Multiplying Matrices Using dgemm
oneMKL provides several routines for multiplying matrices. The most widely used is the dgemm routine, which calculates the product of double precision matrices:
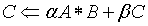
The dgemm routine can perform several calculations. For example, you can perform this operation with the transpose or conjugate transpose of A and B. The complete details of capabilities of the dgemm routine and all of its arguments can be found in the ?gemm topic in the Intel® oneAPI Math Kernel Library Developer Reference.
Use dgemm to Multiply Matrices
This exercise demonstrates declaring variables, storing matrix values in the arrays, and calling dgemm to compute the product of the matrices. The arrays are used to store these matrices:

The one-dimensional arrays in the exercises store the matrices by placing the elements of each column in successive cells of the arrays.
The Fortran source code for this tutorial is shown below.
Although oneMKL supports Fortran 90 and later, the exercises in this tutorial use FORTRAN 77 for compatibility with as many versions of Fortran as possible.
* Fortran source code is found in dgemm_example.f
PROGRAM MAIN
IMPLICIT NONE
DOUBLE PRECISION ALPHA, BETA
INTEGER M, K, N, I, J
PARAMETER (M=2000, K=200, N=1000)
DOUBLE PRECISION A(M,K), B(K,N), C(M,N)
PRINT *, "This example computes real matrix C=alpha*A*B+beta*C"
PRINT *, "using Intel(R) MKL function dgemm, where A, B, and C"
PRINT *, "are matrices and alpha and beta are double precision "
PRINT *, "scalars"
PRINT *, ""
PRINT *, "Initializing data for matrix multiplication C=A*B for "
PRINT 10, " matrix A(",M," x",K, ") and matrix B(", K," x", N, ")"
10 FORMAT(a,I5,a,I5,a,I5,a,I5,a)
PRINT *, ""
ALPHA = 1.0
BETA = 0.0
PRINT *, "Intializing matrix data"
PRINT *, ""
DO I = 1, M
DO J = 1, K
A(I,J) = (I-1) * K + J
END DO
END DO
DO I = 1, K
DO J = 1, N
B(I,J) = -((I-1) * N + J)
END DO
END DO
DO I = 1, M
DO J = 1, N
C(I,J) = 0.0
END DO
END DO
PRINT *, "Computing matrix product using Intel(R) MKL DGEMM "
PRINT *, "subroutine"
CALL DGEMM('N','N',M,N,K,ALPHA,A,M,B,K,BETA,C,M)
PRINT *, "Computations completed."
PRINT *, ""
PRINT *, "Top left corner of matrix A:"
PRINT 20, ((A(I,J), J = 1,MIN(K,6)), I = 1,MIN(M,6))
PRINT *, ""
PRINT *, "Top left corner of matrix B:"
PRINT 20, ((B(I,J),J = 1,MIN(N,6)), I = 1,MIN(K,6))
PRINT *, ""
20 FORMAT(6(F12.0,1x))
PRINT *, "Top left corner of matrix C:"
PRINT 30, ((C(I,J), J = 1,MIN(N,6)), I = 1,MIN(M,6))
PRINT *, ""
30 FORMAT(6(ES12.4,1x))
PRINT *, "Example completed."
STOP
END
This exercise illustrates how to call the dgemm routine. An actual application would make use of the result of the matrix multiplication.
This call to the dgemm routine multiplies the matrices:
CALL DGEMM('N','N',M,N,K,ALPHA,A,M,B,K,BETA,C,M)
The arguments provide options for how oneMKL performs the operation. In this case:
- 'N'
-
Character indicating that the matrices A and B should not be transposed or conjugate transposed before multiplication.
- M, N, K
-
Integers indicating the size of the matrices:
A: M rows by K columns
B: K rows by N columns
C: M rows by N columns
- ALPHA
-
Real value used to scale the product of matrices A and B.
- A
-
Array used to store matrix A.
- M
-
Leading dimension of array A, or the number of elements between successive columns (for column major storage) in memory. In the case of this exercise the leading dimension is the same as the number of rows.
- B
-
Array used to store matrix B.
- K
-
Leading dimension of array B, or the number of elements between successive columns (for column major storage) in memory. In the case of this exercise the leading dimension is the same as the number of rows.
- BETA
-
Real value used to scale matrix C.
- C
-
Array used to store matrix C.
- M
-
Leading dimension of array C, or the number of elements between successive columns (for column major storage) in memory. In the case of this exercise the leading dimension is the same as the number of rows.
Compile and Link Your Code
oneMKL provides many options for creating code for multiple processors and operating systems, compatible with different compilers and third-party libraries, and with different interfaces. To compile and link the exercises in this tutorial with Intel® Parallel Studio XE Composer Edition, type
- Windows* OS: ifort /Qmkl src\dgemm_example.f
- Linux* OS, macOS*: ifort -mkl src/dgemm_example.f
Alternatively, you can use the supplied build scripts to build and run the executables.
- Windows* OS:
build build run_dgemm_example
- Linux* OS, macOS*:
make make run_dgemm_example
For the executables in this tutorial, the build scripts are named:
Example |
Executable |
|---|---|
dgemm_example.f |
run_dgemm_example |
dgemm_with_timing.f |
run_dgemm_with_timing |
matrix_multiplication.f |
run_matrix_multiplication |
dgemm_threading_effect_example.f |
run_dgemm_threading_effect_example |
This assumes that you have installed oneMKL and set environment variables as described in .
For other compilers, use the oneMKL Link Line Advisor to generate a command line to compile and link the exercises in this tutorial: http://software.intel.com/en-us/articles/intel-mkl-link-line-advisor/.
After compiling and linking, execute the resulting executable file, named dgemm_example.exe on Windows* OS or a.out on Linux* OS and macOS*.
Product and Performance Information |
|---|
Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex. Notice revision #20201201 |