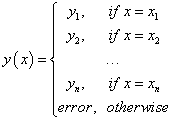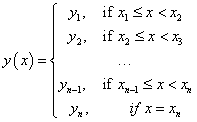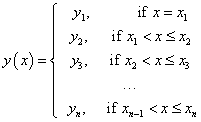Mathematical Conventions for Data Fitting Functions

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 6/30/2025

Version

Public

Mathematical Conventions for Data Fitting Functions

This section explains the notation used for Data Fitting function descriptions. Spline notations are based on the terminology and definitions of [deBoor2001]. The Subbotin quadratic spline definition follows the conventions of [StechSub76]. The quasi-uniform partition definition is based on [Schumaker2007].

Mathematical Notation in the Data Fitting Component
Concept	Mathematical Notation
Partition of interpolation interval [`a`, `b`] , where `x`_i denotes breakpoints. [`x`_i, `x`_i+1) denotes a sub-interval (cell) of size Δ_i=`x`_i+1-`x`_i .	{`x`_i}_i=1,...,n, where `a` = `x`₁ < `x`₂<... <`x`_n = `b`
Quasi-uniform partition of interpolation interval [`a`, `b`]	Partition {`x`_i}_i=1,...,n which meets the constraint with a constant `C` defined as 1 ≤`M`/ `m`≤`C`, where `M` = max_i=1,...,n-1 (Δ_i) `m` = min_i=1,...,n-1 (Δ_i) Δ_i = `x`_i+1 - `x`_i
Vector-valued function of dimension `p` being fit	ƒ(`x`) = (ƒ₁(`x`),..., ƒ_p(`x`))
Piecewise polynomial (PP) function ƒ of order `k+1`	ƒ(`x`) ≔ `P`_i (`x`), if `x` ∈ [ `x`_i, `x`_i+1), `i` = 1,..., `n`-1 where {`x`_i}_{i= 1,..., n} is a strictly increasing sequence of breakpoints. `P`_i(`x`) = `c`_i,0 + `c`_i,1(`x` - `x`_i) + ... + `c`_i,k(`x` - `x`_i)^k is a polynomial of degree `k` (order `k`+1) over the interval `x` ∈ [ `x`_i, `x`_i+1).
Function `p` agrees with function ƒ at the points {`x`_i}_i=1,...,n .	For every point ζ in sequence {`x`_i}_i=1,...,n that occurs `m` times, the equality `p`^(i-1)(ζ) = ƒ^(i-1)(ζ) holds for all `i` = 1,...,`m`, where `p`⁽ⁱ⁾(`t`) is the derivative of the `i`-th order.
The `k`-th divided difference of function ƒ at points `x`_i,..., `x`_{i + k}. This difference is the leading coefficient of the polynomial of order `k`+1 that agrees with ƒ at `x`_i,..., `x`_{i + k}.	[ `x`_i,..., `x`_{i + k}] ƒ In particular, [`x`₁]ƒ = ƒ(`x`₁) [ `x`₁, `x`₂] ƒ = (ƒ(`x`₁) - ƒ(`x`₂)) / (`x`₁ - `x`₂)
A `k`-order derivative of interpolant ƒ(`x`) at interpolation site .

Interpolants to the Function ƒ at `x`₁,..., `x`_n and Boundary Conditions
Concept	Mathematical Notation
Linear interpolant	`P`_i(`x`) = `c`_{1, i} + `c`_{2, i}(`x` - `x`_i), where `x` ∈ [ `x`_i, `x`_i+1) `c`_{1, i} = ƒ(`x`_i) `c`_{2, i} = [`x`_i, `x`_i+1 ]ƒ `i` = 1,..., `n`-1
Piecewise parabolic interpolant	`P`_i(`x`) = `c`_{1, i} + `c`_{2, i}(`x` - `x`_i) + `c`_{3, i}(`x` - `x`_i)², `x` ∈ [ `x`_i, `x`_i+1) Coefficients `c`_{1, i}, `c`_{2, i}, and `c`_{3, i} depend on the conditions: `P`_i(`x`_i) = ƒ(`x`_i) `P`_i(`x`_i+1) = ƒ(`x`_i+1) `P`_i((`x`_i+1 + `x`_i) / 2) = `v`_i+1 where parameter `v`_i+1 depends on the interpolant being continuously differentiable: `P`_i-1⁽¹⁾(`x`_i) = `P`_i⁽¹⁾(`x`_i)
Piecewise parabolic Subbotin interpolant	`P`(`x`) = `P`_i(`x`) = `c`_1,i+`c`_2,i(`x`-`x`_i)+`c`_3,i(`x`-`x`_i)²+`d`_3,i((`x`-`t`_i)₊)², where `x` ∈ [ `t`_i, `t`_i+1) {`t`_i}_i=1,...,n+1 is a sequence of knots such that `t`₁ = `x`₁, `t`_n+1 = `x`_n `t`_i ∈ (`x`_i-1, `x`_i), `i` = 2,..., `n` Coefficients `c`_1,i, `c`_2,i, `c`_3,i, and `d`_3,i depend on the following conditions: `P`_i(`x`_i) = ƒ(`x`_i), `P`_i(`x`_i+1) = ƒ(`x`_i+1) `P`(`x`) is a continuously differentiable polynomial of the second degree on [ `t`_i, `t`_i+1), `i` = 1,..., `n`.
Piecewise cubic Hermite interpolant	`P`_i(`x`) = `c`_1,i + `c`_2,i(`x` - `x`_i) + `c`_3,i(`x` - `x`_i)² + `c`_4,i(`x` - `x`_i)³, where `x` ∈ [ `x`_i, `x`_i+1) `c`_1,i = ƒ(`x`_i) `c`_2,i = `s`_i `c`_3,i = ([`x`_i, `x`_i+1]ƒ - `s`_i ) / (Δ`x`_i) - `c`_4,i(Δ`x`_i) `c`_4,i = (`s`_i + `s`_i+1 - 2[`x`_i, `x`_i+1]ƒ) / (Δ`x`_i)² `i` = 1,..., `n`-1 `s`_i = ƒ⁽¹⁾(`x`_i)
Piecewise cubic Bessel interpolant	`P`_i(`x`) = `c`_1,i + `c`_2,i(`x` - `x`_i) + `c`_3,i(`x` - `x`_i)² + `c`_4,i(`x` - `x`_i)³, where `x` ∈ [ `x`_i, `x`_i+1) `c`_1,i = ƒ(`x`_i) `c`_2,i = `s`_i `c`_3,i = ([`x`_i, `x`_i+1]ƒ - `s`_i ) / (Δ`x`_i) - `c`_4,i(Δ`x`_i) `c`_4,i = (`s`_i + `s`_i+1 - 2[`x`_i, `x`_i+1]ƒ) / (Δ`x`_i)² `i` = 1,..., `n`-1 `s`_i = (Δ`x`_i[`x`_i-1, `x`_i]ƒ + Δ`x`_i-1[`x`_i, `x`_i+1]ƒ) / (Δ`x`_i + Δ`x`_i+1)
Piecewise cubic Akima interpolant	`P`_i(`x`) = `c`_1,i + `c`_2,i(`x` - `x`_i) + `c`_3,i(`x` - `x`_i)² + `c`_4,i(`x` - `x`_i)³, where `x` ∈ [ `x`_i, `x`_i+1) `c`_1,i = ƒ(`x`_i) `c`_2,i = `s`_i `c`_3,i = ([`x`_i, `x`_i+1]ƒ - `s`_i ) / (Δ`x`_i) - `c`_4,i(Δ`x`_i) `c`_4,i = (`s`_i + `s`_i+1 - 2[`x`_i, `x`_i+1]ƒ) / (Δ`x`_i)² `i` = 1,..., `n`-1 `s`_i = (`w`_i+1[`x`_i-1, `x`_i]ƒ + `w`_i-1[`x`ƒ_i, `x`_i+1]ƒ) / (`w`_i+1 + `w`_i-1), where `w`_i = \|[`x`_i, `x`_i+1]ƒ - [`x`_i-1, `x`_i]ƒ\|
Piecewise natural cubic interpolant	`P`_i(`x`) = `c`_1,i + `c`_2,i(`x` - `x`_i) + `c`_3,i(`x` - `x`_i)² + `c`_4,i(`x` - `x`_i)³, where `x` ∈ [ `x`_i, `x`_i+1) `c`_1,i = ƒ(`x`_i) `c`_2,i = `s`_i `c`_3,i = ([`x`_i, `x`_i+1]ƒ - `s`_i ) / (Δ`x`_i) - `c`_4,i(Δ`x`_i) `c`_4,i = (`s`_i + `s`_i+1 - 2[`x`_i, `x`_i+1]ƒ) / (Δ`x`_i)² `i` = 1,..., `n`-1 Parameter `s`_i depends on the condition that the interpolant is twice continuously differentiable: `P`_i-1⁽²⁾(`x`_i) = `P`_i⁽²⁾(`x`_i).
Not-a-knot boundary condition.	Parameters `s`₁ and `s`_n provide `P`₁ = `P`₂ and `P`_n-1 = `P`_n, so that the first and the last interior breakpoints are inactive.
Free-end boundary condition.	ƒ^"(`x`₁) = ƒ^"(`x`_n) = 0
Look-up interpolator for discrete set of points (`x`₁, `y`₁),..., (`x`_n, `y`_n) .
Step-wise constant continuous right interpolator.
Step-wise constant continuous left interpolator.

Parent topic: Data Fitting Functions

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Mathematical Conventions for Data Fitting Functions