Using the Black-Scholes formula for European options pricing
Goal
Speed up Black-Scholes computation of European options pricing.
Solution
Use oneMKL vector math functions to speed up computation.
The Black-Scholes model describes the market behavior as a system of stochastic differential equations [Black73]. Call and put European options issued in this market are then priced according to the Black-Scholes formulae:
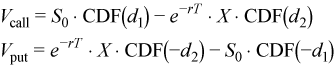
where
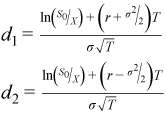
Vcall /Vput are the present values of the call/put options,S0 is the present price of the stock , X is the strike price, r is the risk-neutral rate, σ is the volatility, T is the maturity and CDF is the cumulative distribution function of the standard normal distribution.
Alternatively, you can use the error function ERF which has a simple relationship with the cumulative normal distribution function:
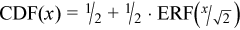
Source code: see the black-scholes folder in the samples archive available at https://www.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip.
Straightforward implementation of Black-Scholes
This code implements the closed form solution for pricing call and put options.
void BlackScholesFormula( int nopt,
tfloat r, tfloat sig, const tfloat s0[], const tfloat x[],
const tfloat t[], tfloat vcall[], tfloat vput[] )
{
tfloat d1, d2;
int i;
for ( i=0; i<nopt; i++ )
{
d1 = ( LOG(s0[i]/x[i]) + (r + HALF*sig*sig)*t[i] ) /
( sig*SQRT(t[i]) );
d2 = ( LOG(s0[i]/x[i]) + (r - HALF*sig*sig)*t[i] ) /
( sig*SQRT(t[i]) );
vcall[i] = s0[i]*CDFNORM(d1) - EXP(-r*t[i])*x[i]*CDFNORM(d2);
vput[i] = EXP(-r*t[i])*x[i]*CDFNORM(-d2) - s0[i]*CDFNORM(-d1);
}
}
The number of options is specified as the nopt parameter. The tfloat type is either float or double depending on the precision you want to use. Similarly LOG , EXP , SQRT, and CDFNORM map to single or double precision versions of the respective math functions. The constant HALF is either 0.5f or 0.5 for single and double precision, respectively.
In addition to nopt, the input parameters for the algorithm are s0 (present stock price), r (risk-neutral rate), sig (volatility), t (maturity), and x (strike price). The result is returned in vcall and vput (the present value of the call and put options, respectively).
It is assumed that r and sig are constant for all options being priced; the other parameters are arrays of floating-point values. The vcall and vput parameters are output arrays.
Discussion
Transcendental functions are at the core of the Black-Scholes formula benchmark. However, each option value depends on five parameters and as the math is computed faster, the memory effects become more pronounced. Thus the number of array parameters is an important factor that can change the computations from being compute-limited to memory bandwidth limited. Additionally, memory size constraints should be considered when pricing hundred millions of options.
The Intel C++ Compiler provides vectorization and parallelization controls that might help uncover the SIMD and multi-core potential of Intel Architecture with respect to the Black-Scholes formula. Optimized vectorized math functionality is available with the Short Vector Math Library (SVML) runtime library.
The oneMKL Vector Mathematical (VM) functions provide highly tuned transcendental math functionality that can be used to further speed up formula computations.
There are several opportunities for optimization of the straightforward code: hoisting common sub-expressions out of loops, replacing the CDFNORM function with the ERF function (which is usually faster), exploiting the relationship ERF(-x) = -ERF(x), and replacing the division by SQRT with multiplication by the reciprocal square root INVSQRT (which is usually faster).
Optimized implementation of Black-Scholes
void BlackScholesFormula( int nopt,
tfloat r, tfloat sig, tfloat s0[], tfloat x[],
tfloat t[], tfloat vcall[], tfloat vput[] )
{
int i;
tfloat a, b, c, y, z, e;
tfloat d1, d2, w1, w2;
tfloat mr = -r;
tfloat sig_sig_two = sig * sig * TWO;
for ( i = 0; i < nopt; i++ )
{
a = LOG( s0[i] / x[i] );
b = t[i] * mr;
z = t[i] * sig_sig_two;
c = QUARTER * z;
e = EXP ( b );
y = INVSQRT( z );
w1 = ( a - b + c ) * y;
w2 = ( a - b - c ) * y;
d1 = ERF( w1 );
d2 = ERF( w2 );
d1 = HALF + HALF*d1;
d2 = HALF + HALF*d2;
vcall[i] = s0[i]*d1 - x[i]*e*d2;
vput[i] = vcall[i] - s0[i] + x[i]*e;
}
}
In this code INVSQRT(x) is either 1.0/sqrt(x) or 1.0f/sqrtf(x) depending on precision; TWO and QUARTER are the floating-point constants 2 and 0.25 respectively.
Discussion
A few optimizations help generating effective code using the Intel® C/C++ compiler. See the User and Reference Guide for the Intel® C++ Compiler for more details about the compiler pragmas and switches suggested in this section.
Apply #pragma simd to tell the compiler to vectorize the loop and #pragma vector aligned to notify the compiler that the arrays are aligned (you need to properly align vectors at the memory allocation stage) and that it is safe to rely on aligned load and store instructions. Efficient vectorization, such as that available with SVML, can achieve a speedup of several times versus scalar code.
…
#pragma simd
#pragma vector aligned
for ( i = 0; i < nopt; i++ )
…
With these changes the code can take advantage of all available CPU cores. The simplest way is to add the -autopar switch to the compilation line so that the compiler attempts to parallelize the code automatically. Another option is to use the standard OpenMP* pragma:
…
#pragma omp parallel for
for ( i = 0; i < nopt; i++ )
…
Further performance improvements are possible if you can relax the accuracy of math functions using Intel C++ Compiler options such as -fp-model fast, -no-prec-div, -ftz, -fimf-precision, -fimf-max-error, and -fimf-domain-exclusion.
Linux* OS specific syntax is given for the compiler switches. See the User and Reference Guide for the Intel® C++ Compiler for more detail.
In massively parallel cases, the compute time of math functions can be low enough for memory bandwidth to emerge as the limiting factor for loop performance. This can impair the otherwise linear speedup from parallelism. In such cases memory bandwidth friendly non-temporal load/store instructions can help:
…
#pragma vector nontemporal
for ( i = 0; i < nopt; i++ )
…
The oneMKL VM component provides highly tuned transcendental math functions that can help further improving performance. However, using them requires refactoring of the code to accommodate for the vector nature of the VM APIs. In the following code example, non-trivial math functions are taken from VM, while remaining basic arithmetic is left to the compiler.
A temporary buffer is allocated on the stack of the function to hold intermediate results of vector math computations. It is important for the buffer to be aligned on the maximum applicable SIMD register size. The buffer size is chosen to be large enough for the VM functions to achieve their best performance (compensating for vector function startup cost), yet small enough to maximize cache residence of the data. You can experiment with buffer size; a suggested starting point is NBUF=1024.
oneMKL VM implementation of Black-Scholes
void BlackScholesFormula_MKL( int nopt,
tfloat r, tfloat sig, tfloat * s0, tfloat * x,
tfloat * t, tfloat * vcall, tfloat * vput )
{
int i;
tfloat mr = -r;
tfloat sig_sig_two = sig * sig * TWO;
#pragma omp parallel for \
shared(s0, x, t, vcall, vput, mr, sig_sig_two, nopt) \
default(none)
for ( i = 0; i < nopt; i+= NBUF )
{
int j;
tfloat *a, *b, *c, *y, *z, *e;
tfloat *d1, *d2, *w1, *w2;
__declspec(align(ALIGN_FACTOR)) tfloat Buffer[NBUF*4];
// This computes vector length for the last iteration of the loop
// in case nopt is not exact multiple of NBUF
#define MY_MIN(x, y) ((x) < (y)) ? (x) : (y)
int nbuf = MY_MIN(NBUF, nopt - i);
a = Buffer + NBUF*0; w1 = a; d1 = w1;
c = Buffer + NBUF*1; w2 = c; d2 = w2;
b = Buffer + NBUF*2; e = b;
z = Buffer + NBUF*3; y = z;
// Must set VM accuracy in each thread
vmlSetMode( VML_ACC );
VDIV(nbuf, s0 + i, x + i, a);
VLOG(nbuf, a, a);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
b[j] = t[i + j] * mr;
a[j] = a[j] - b[j];
z[j] = t[i + j] * sig_sig_two;
c[j] = QUARTER * z[j];
}
VINVSQRT(nbuf, z, y);
VEXP(nbuf, b, e);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
tfloat aj = a[j];
tfloat cj = c[j];
w1[j] = ( aj + cj ) * y[j];
w2[j] = ( aj - cj ) * y[j];
}
VERF(nbuf, w1, d1);
VERF(nbuf, w2, d2);
#pragma simd
for ( j = 0; j < nbuf; j++ )
{
d1[j] = HALF + HALF*d1[j];
d2[j] = HALF + HALF*d2[j];
vcall[i+j] = s0[i+j]*d1[j] - x[i+j]*e[j]*d2[j];
vput[i+j] = vcall[i+j] - s0[i+j] + x[i+j]*e[j];
}
}
}
For comparable precisions, oneMKL VM can deliver 30-50% better performance versus Intel Compiler and SVML-based solutions if the problem is compute bound (the data fits in the L2 cache). In this case the latency of cache read/write operations is masked by computations. Once the memory bandwidth emerges as a factor with the growth of the problem size, it becomes more important to optimize the memory usage, and the Intel VM solution based on intermediate buffers can lose its advantage to the no-buffering one-pass solution with SVML.
Routines Used
Task |
Routine |
|---|---|
Sets a new accuracy mode for VM functions according to the mode parameter and stores the previous VM mode to oldmode. |
vmlSetMode |
Performs element by element division of vector a by vector b |
vsdiv/vddiv |
Computes natural logarithm of vector elements. |
vsln/vdln |
Computes an inverse square root of vector elements. |
vsinvsqrt/vdinvsqrt |
Computes an exponential of vector elements. |
vsexp/vdexp |
Computes the error function value of vector elements. |
vserf/vderf |