NumPy UMath Optimizations
One of the great benefits found in our Intel® Distribution for Python is the performance boost gained from leveraging SIMD and multithreading in (select) NumPy’s UMath arithmetic and transcendental operations, on a range of Intel CPUs, from Intel® Core™ to Intel® Xeon™ & Intel® Xeon Phi™. With stock python as our baseline, we demonstrate the scalability of Intel® Distribution for Python by using functions that are intensively used in financial math applications and machine learning:
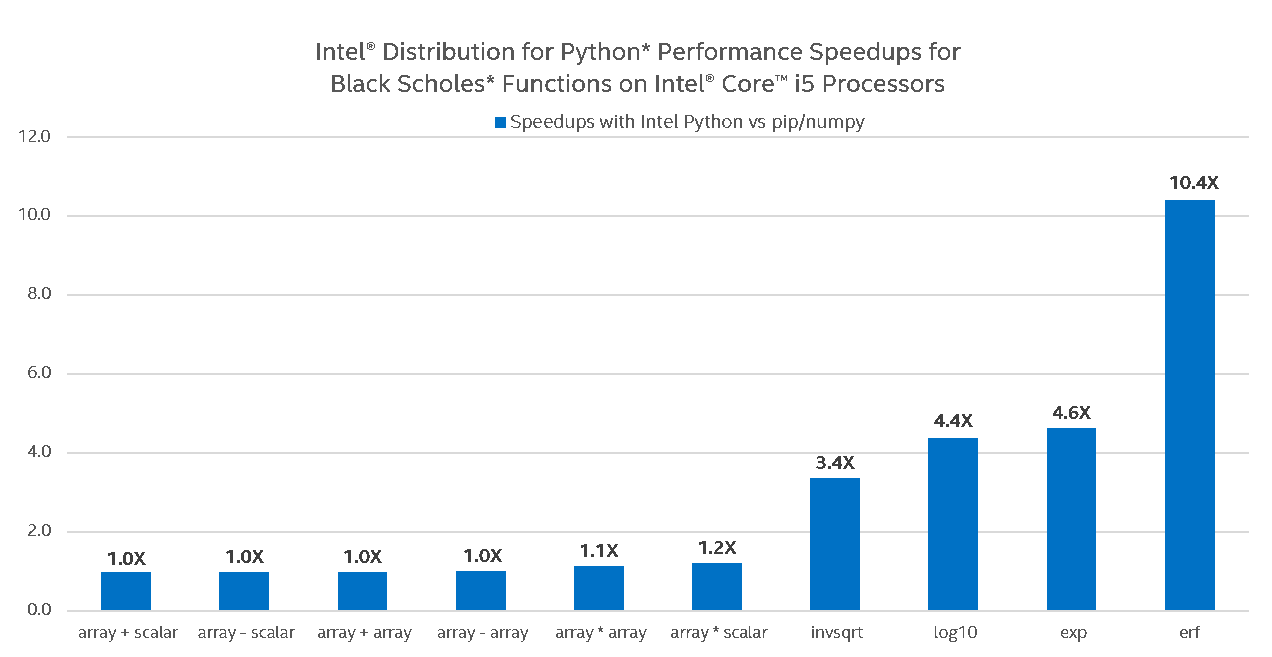
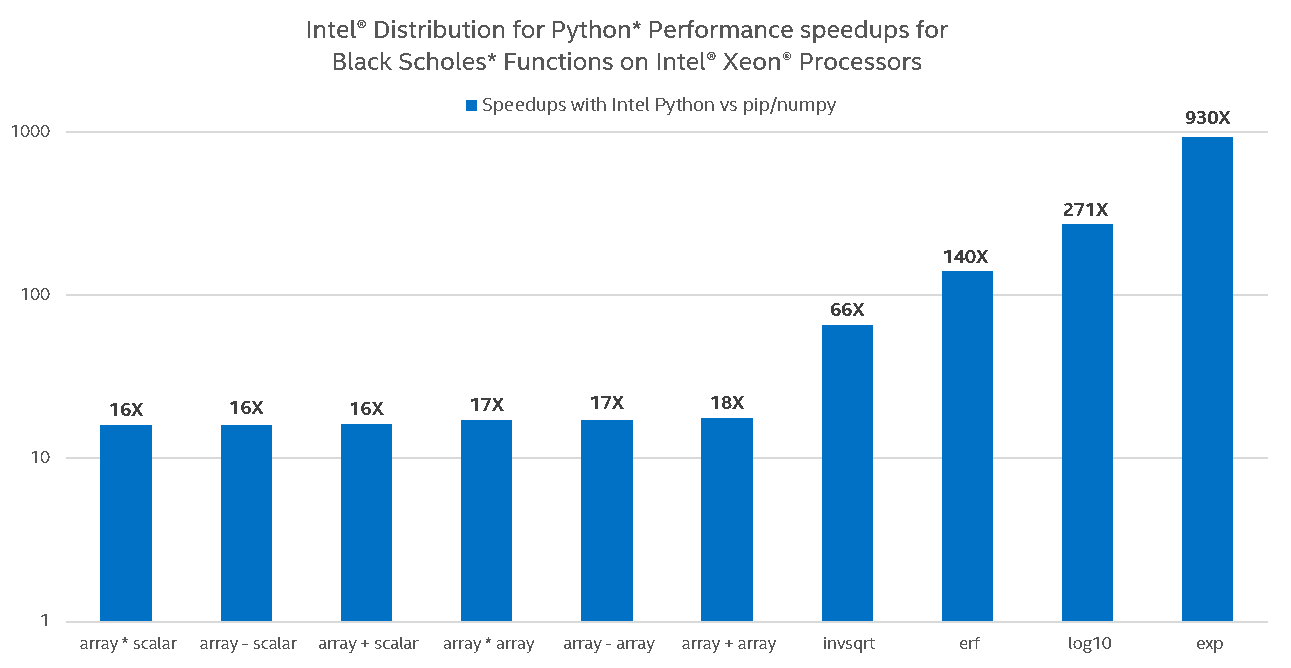
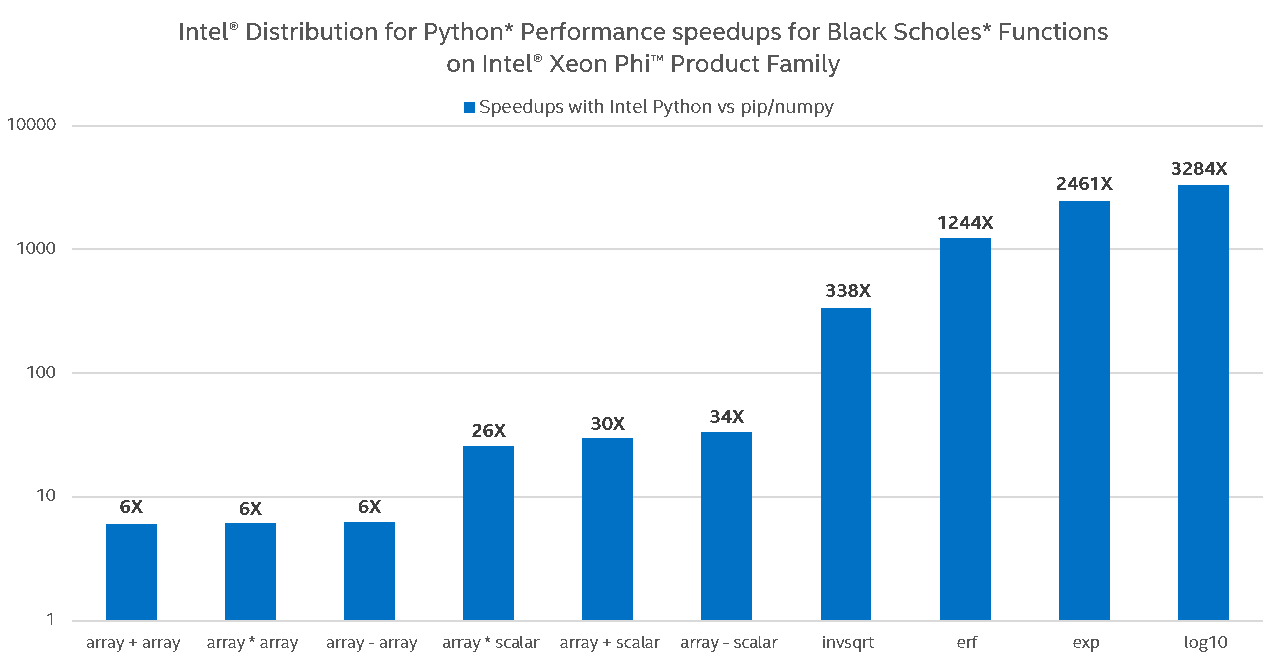
One can see that stock Python (pip-installed NumPy from PyPI) on Intel® Core™ i5 performs basic operations such as addition, subtraction, and multiplication just as well as Intel Python, but not on Intel® Xeon™ and Intel® Xeon Phi™, where Intel Python adds at least another 10x speedup. This can be explained by the fact that basic arithmetic operations in stock NumPy are hard-coded AVX intrinsics (and thus already leverage SIMD, but do not scale to other ISA, e.g. AVX-512). These operations in stock Python also do not leverage multiple cores (i.e. no multi-threading of loops under the hood of NumPy exist with such operations). Intel Python’s implementation allows for this scalability by utilizing the following: respective Intel® MKL VML primitives, which are CPU-dispatched (to leverage appropriate ISA) and multi-threaded (leverage multiple cores) under the hood, and Intel® SVML intrinsics, a compiler-provided short vector math library that vectorizes math functions for both IA-32 and Intel® 64-bit architectures on supported operating systems. Depending on the problem size, NumPy will choose one of the two approaches. On much smaller array sizes, Intel® SVML outperforms VML due to VML’s inherent cost of setting up the environment to multi-thread loops. For any other problem size, VML outperforms SVML and this is thanks to VML’s ability to both vectorize math functions and multi-thread loops.
Specifically, on Intel® Core® i5 Intel Python delivers greater performance on transcendentals (log, exp, erf, etc.) due to utilizing both SIMD and multi-threading. We do not see any visible benefit of multi-threading basic operations (as shown on the graph) unless NumPy arrays are very large (not shown on the graph). On Xeon®, the 10x-1000x boost is explained by leveraging both (a) AVX2 instructions in transcendentals and (b) multiple cores (32 in our setup). Even greater scalability of Xeon Phi® relative to Xeon is explained by larger number of cores (64 in our setup) and a wider SIMD.
The following charts provide another view of Intel Python performance versus stock Python on arithmetic and transcendental vector operations in NumPy by measuring how close UMath performance is to respective native MKL call:
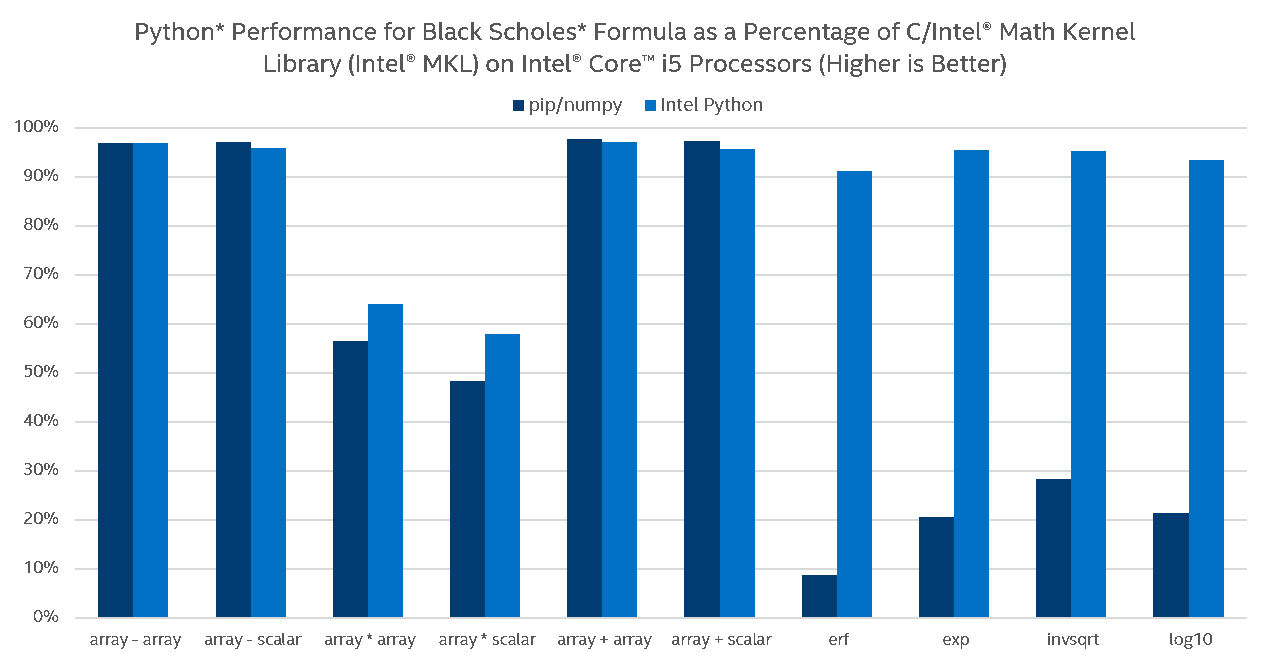
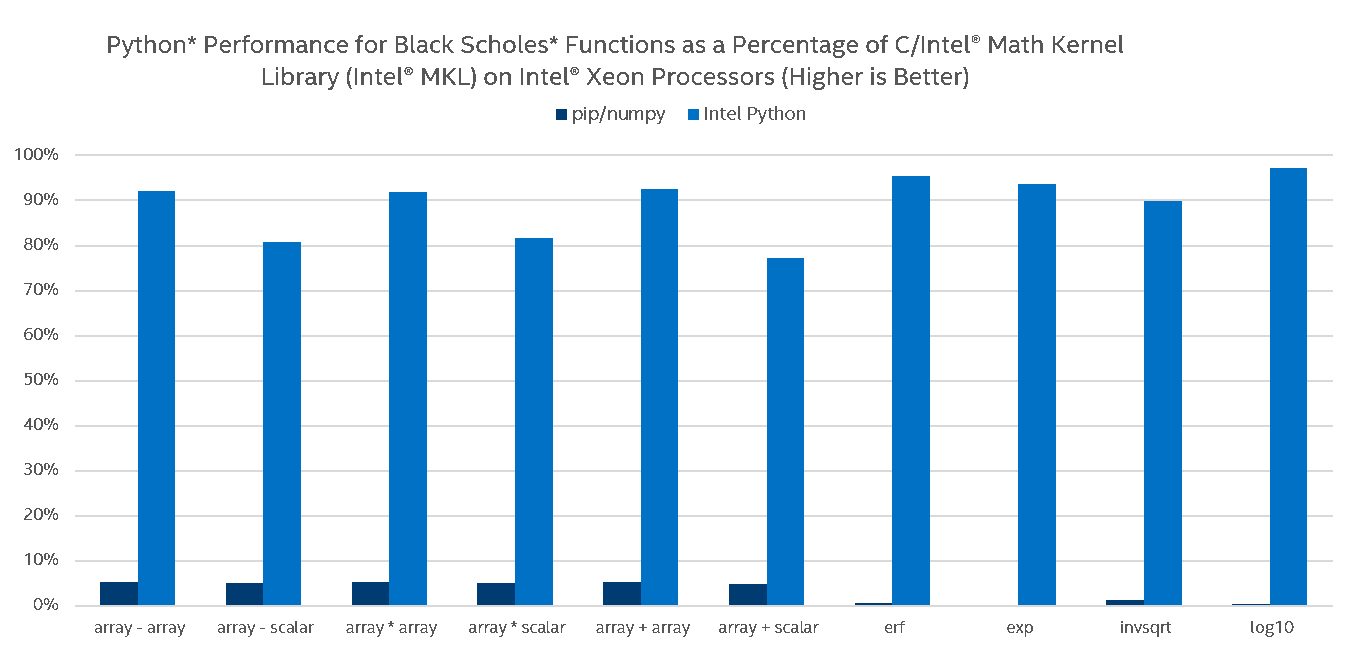
Again, on Intel® Core™ i5, the stock Python performs well on basic operations (due to hard-coded AVX intrinsics and because multi-threading from Intel Python does not add much on basic operations) but does not scale on transcendentals (loops with transcendentals are not vectorized in stock Python). Intel Python delivers performance close to native speeds (90% of MKL) on relatively big problem sizes. While running our umath optimization benchmarks on different architectures, it was discovered that the performance of the umath functions did not scale as one would expect on the Intel® Xeon Phi™. We identified an issue with Intel® OpenMP that made the MKL VML function calls perform poorly in multiprocessing mode. Our team is working closely with the Intel® MKL and Intel® OpenMP teams to resolve this issue.
To demonstrate the benefits of vectorization and multi-threading in a real-world application, we chose to use the Black Scholes model, used to estimate the price of financial derivatives, specifically European vanilla stock options. A Python implementation of the Black Scholes formula gives an idea of how NumPy UMath optimizations can be noticed at the application level:
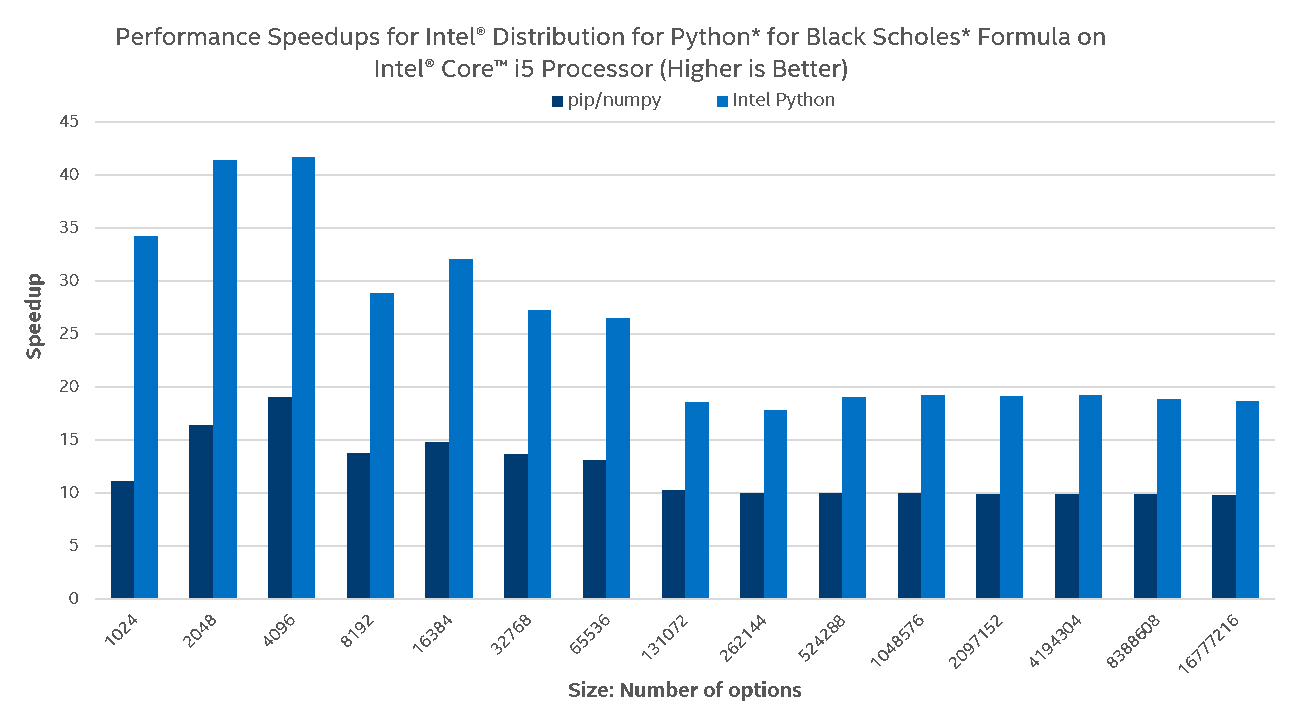
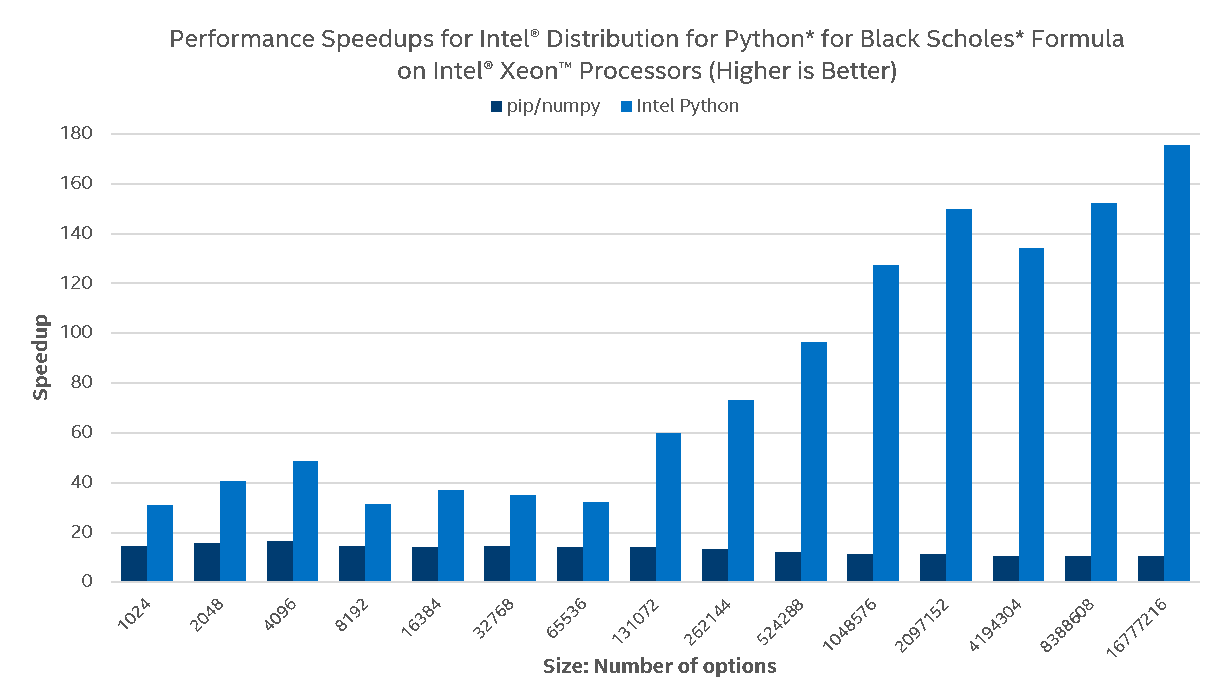
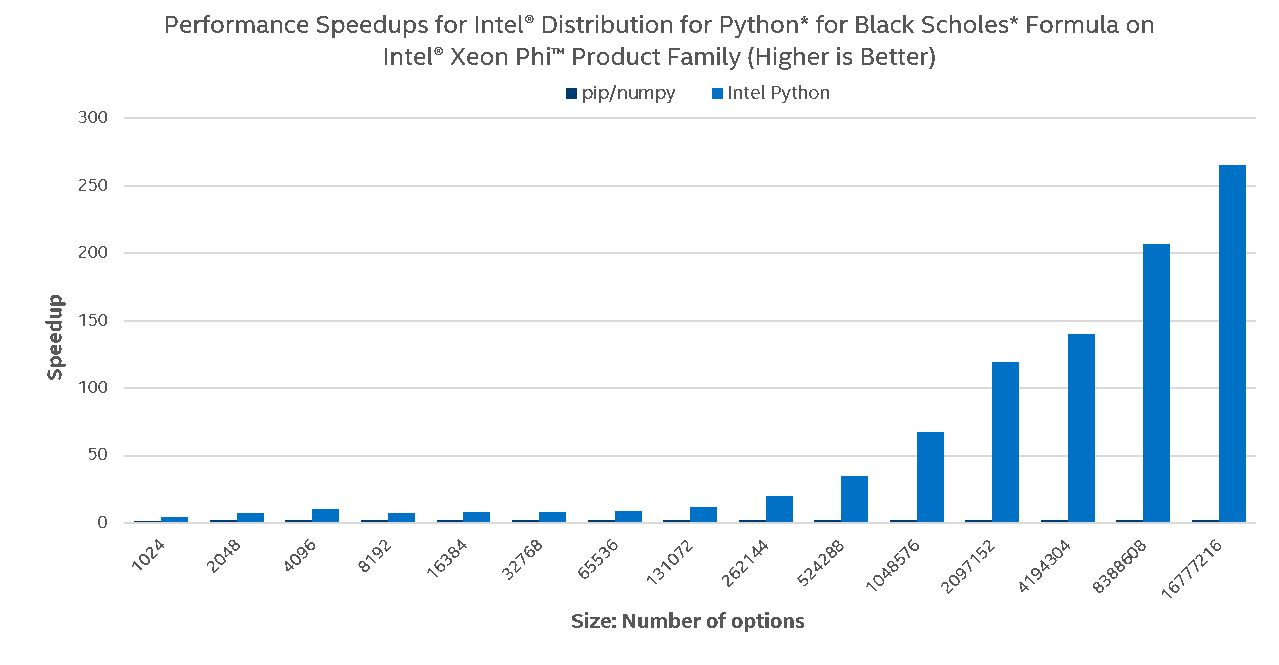
One can see that on Intel® Core™ i5, the Black Scholes Formula scales nicely with Intel Python on small problem sizes but does not perform well on bigger problem sizes, which is explained by small cache sizes. Stock Python does marginally scale due to leveraging AVX instructions on basic arithmetic operations, but this is a whole different story on Intel® Xeon™ and Intel® Xeon Phi™. With Intel Python running the same Python code on server processors, much greater scalability on much greater problem sizes is delivered. Intel® Xeon Phi™ scales better due to bigger number of cores and as expected, the stock Python does not scale on server processors due to the lack of AVX2/AVX-512 support for transcendentals and no multi-threading utilization.