Introduction
Intel® Math Kernel Library (Intel® MKL) presents new parallel solution for large sparse SVD problem. Functionality is based on subspace iteration method combined with recent techniques that estimate eigenvalue counts [1]. The idea of underlying algorithm is to split the interval that contains all singular values into subintervals with close to an equal number of values and apply a polynomial filter on each of the subintervals in parallel. This approach allows to solve problems of size up to 10^6 and enables multiple levels of parallelism.
This functionality is now available for non-commercial use as a separate package that must be linked with installed Intel MKL version. Current version of package supports two functions:
- Shared memory SVD. Supports parallelization in Open MP.
- Cluster version of SVD. This realization supports MPI parallelization of the independent subproblems defined by each subinterval and matrix operations within each subinterval are Open MP parallel.
Support of the trial package is now limited to linux/windows 64-bit Architectures with only C interface. In future, these limitations will be removed.
Product Overview
Problem statement: Compute several largest/smallest singular values and corresponding (right/left) singular vectors.
Unlike available in Intel MKL LAPACK and SCALAPACK ?gesvd and p?gesvd functionality [2,3], new package supports sparse input matrix and only part of largest/smallest singular values on output, thus allowing to solve problems of larger size more efficiently. Current implementation supports input matrix in CSR format and dense singular vectors on output. Customer must specify number of largest/smallest singular values to find as well as desired tolerance of solution. Number of singular values in question can be up to the size of matrix. However, it is up to customer to ensure that enough space is available to store dense output for singular vectors. On output, each MPI rank will store its part of singular values and singular vectors.
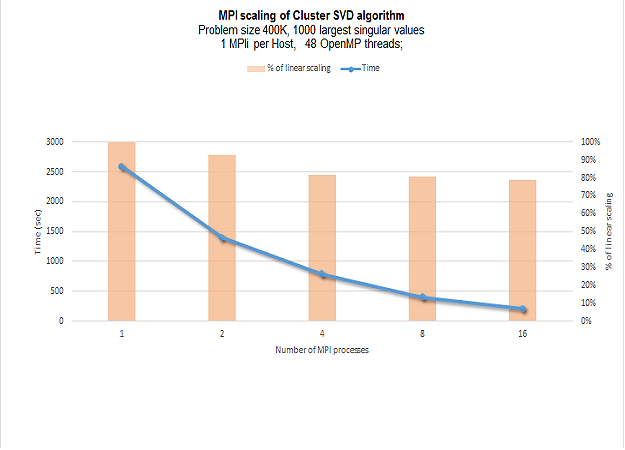
The chart below shows MPI scalability for Cluster SVD solver on randomly generated matrix of size 4*10^5 with 1000 largest singular values requested. Chart shows that almost linear scalability is achieved over many MPI processes.
The attached C examples demonstrate how to make these computations.
Please let us know in the case if you would like to take this evaluation package.
[1] E. Di Napoli, E. Polizzi, Y. Saad, Efficient Estimation of Eigenvalue Counts in an Interval