Because of their remarkable accuracy and performance, deep neural networks (DNNs) have become an essential component in various safety critical applications such as medical diagnosis, self-driving cars, weather predictions, etc. However, they often suffer from overfitting the training data and being overconfident in their predictions, even when they are wrong. This limitation restricts their ability to detect out-of-distribution data or provide information about the uncertainty of their predictions, including reliable confidence intervals. This issue is critical in real-world applications, where explainability and safety are required. For example, in medical diagnosis, the model should provide an uncertainty measure with its predictions.
Unlike conventional DNN models that aim to find deterministic point estimates for weight parameters that fit the data best, Bayesian deep neural network (BNN) models aim to learn the posterior distribution over weights based on Bayes’ theorem (Figure 1). The weights of the Bayesian models are sampled from the learned distribution during inference, enabling the estimation of predictive uncertainty through multiple Monte Carlo samples.
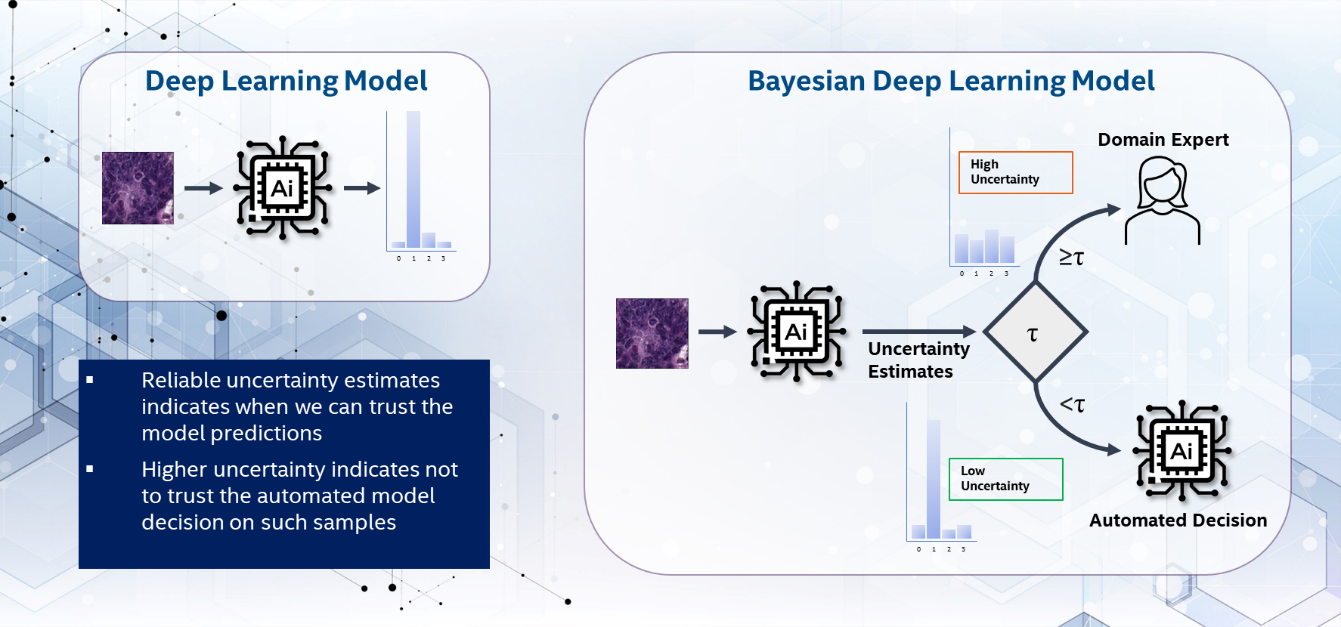
Figure 1. Uncertainty-guided selective prediction in colorectal histology diagnostics
BNNs require additional memory and computational cost because of weight sampling and multiple stochastic forward passes, which leads larger model size and slower inference compared to deterministic models. These drawbacks create a significant challenge in deploying BNNs in real-world applications. This is where quantization comes into play. Quantization can be useful to reduce memory and computational cost of BNN inference by representing the weights and activations with low-precision data types, like 8-bit integers (int8).
Here, we will introduce a Bayesian deep learning (BDL) workload with a quantized model built using Bayesian-Torch, a widely used PyTorch*-based open-source library for BDL. It supports low-precision optimization of BDL. Using Bayesian-Torch, we deployed quantized Bayesian models on the 4th Gen Intel® Xeon® scalable processor with Intel® Advanced Matrix Extensions (Intel® AMX), achieving an inference speedup of 6.9x on the ImageNet benchmark compared to the full-precision Bayesian models, without sacrificing the model accuracy and quality of uncertainty.
Quantization of BNNs
Bayesian-Torch enables seamless conversion of any DNN model to BNN using a simple API (dnn_to_bnn()). We have introduced a comprehensive quantization workflow in our upcoming paper, “Quantization for Bayesian Deep Learning: Low-Precision Characterization and Robustness,” which will be presented at IISWC 2023 (IEEE International Symposium on Workload Characterization). There are three simple steps to apply post-training quantization (PTQ) to BNN:
- Prepare: Prepare the model for static quantization by performing preprocessing tasks such as “Inserting Observers.”
- Calibrate: Calibrate using representative data to obtain calibration statistics.
- Convert: Convert the full-precision Bayesian models into quantized models by calculating scales and zero points for all tensors and operations in the model, as well as replacing quantizable functions with low-precision functions.
The Bayesian-Torch quantization framework has a high-level API that is like PyTorch (Figure 2).

Figure 2. Steps to implement post-training quantization in Bayesian-Torch
Experiments on ResNet-50 with the ImageNet Benchmark
We trained a Bayesian ResNet50 model with mean-field variational inference by specifying the weight priors and initializing the posterior distribution using the empirical Bayes approach. The weight priors are initialized from the pretrained ResNet50 deterministic model available in the Torchvision library. The model is trained using Bayesian-Torch and PyTorch 2.0 on the ImageNet-1K dataset for 50 epochs using SGD optimizer with initial learning rate of 0.0001, momentum of 0.9, and weight decay of 0.0001. We perform post-training quantization on the trained model as previously described to obtain the quantized Bayesian Neural Network (QBNN).
All experiments were performed on the 4th Gen Intel Xeon Scalable processor, which offers built-in acceleration for AI workloads through Intel AMX. Intel AMX supports INT8 precision for inference and Bfloat16 for inference and training. It is a new 64-bit programming paradigm that consists of two components: a set of 2-dimensional registers (or tiles) capable of holding sub-matrices from larger matrices in memory and a tile matrix multiply accelerator. This allows a single instruction to be executed in multiple cycles on the tile and accelerator hardware.
To demonstrate the advantages of the quantized Bayesian model, we compared the inference throughput of the Bayesian ResNet50 model before and after quantization with one Monte Carlo sample on the ImageNet-1K dataset (Table 1). These results show that the quantized Bayesian model has higher throughput than the full-precision Bayesian model, achieving up to 6.9x speedup. This is achieved with a negligible loss of accuracy and no decrease in quality of uncertainty, as quantified by the expected uncertainty calibration error (Table 2).
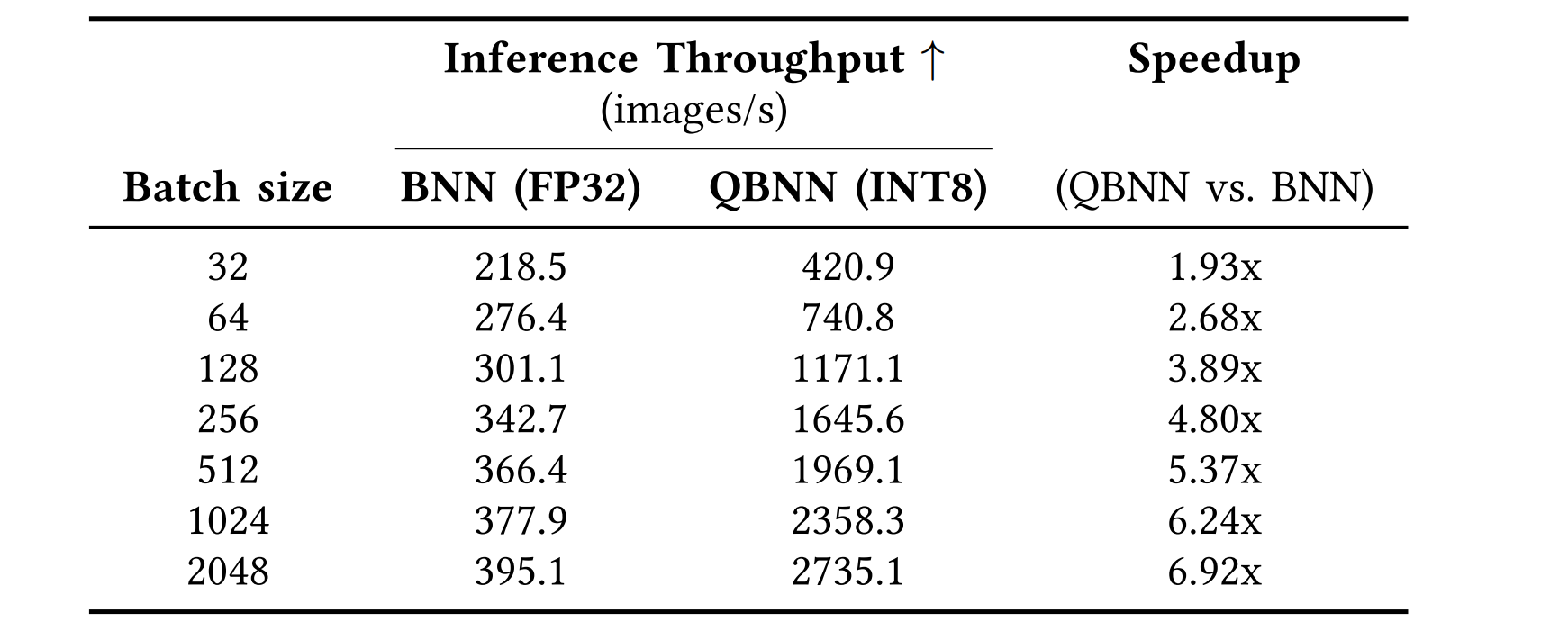
Table 1. Inference throughput comparison of BNN and QBNN on ImageNet-1K across various batch sizes
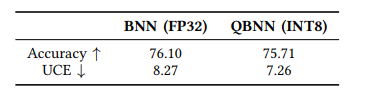
Table 2. Accuracy and uncertainty calibration error of BNN and QBNN on ImageNet. The arrows indicate whether higher or lower is better.
Real-World Safety-Critical Application
We evaluate the proposed quantization framework for a BNN used for medical diagnosis; specifically, colorectal histology image classification. This dataset is a collection of textures in 5,000 histological images of human colorectal cancer. We used 4,000 images for training and 1,000 for testing. Each RGB image is 150 x 150 x 3. The model must classify images into one of eight classes. We trained DNN and BNN models of ResNet-50 architecture for 50 epochs using the SGD optimizer with an initial learning rate of 0.0001, momentum of 0.9, and weight decay of 0.0001. Then, we apply post-training quantization on the trained model to obtain the QBNN model. We evaluated the robustness and reliability of BNN, as well as the quality of uncertainty after quantization on selective prediction and out-of-distribution (OOD) detection tasks described below.
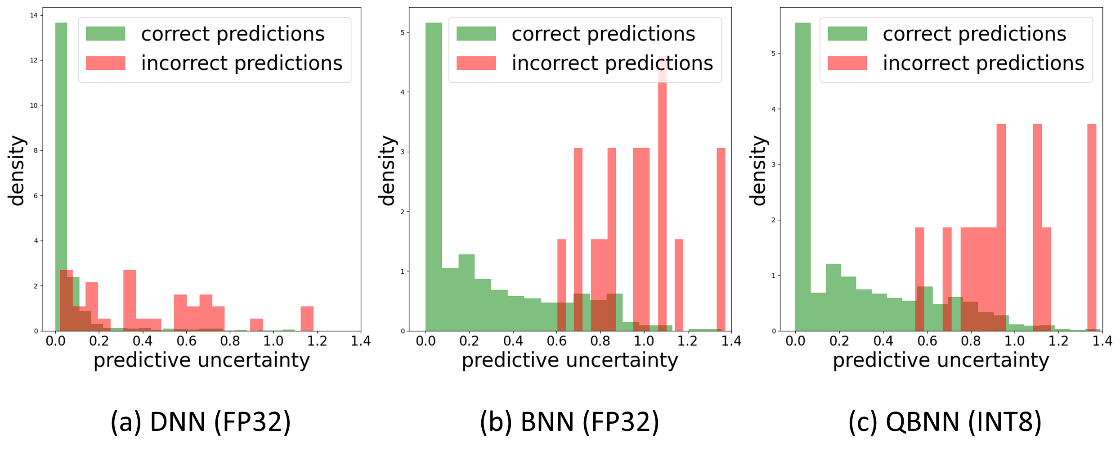
Figure 3. Density histogram of predictive uncertainty for correct and incorrect predictions
We perform uncertainty-guided selective prediction (as shown in Figure 1) where the most uncertain predictions are referred to a domain expert, and the model is evaluated on remaining confident predictions. Figure 3 shows the density histogram of predictive uncertainty obtained from DNN, BNN, and QBNN for correct and incorrect predictions. It is desirable for a model to yield higher uncertainty when it makes incorrect predictions and lower uncertainty associated with correct predictions. We notice that the Bayesian model yields reliable uncertainty estimates compared to DNN, allowing AI practitioners to know when the model may fail. Furthermore, it can be noted from Figure 3(c) that the quality of uncertainty estimation is unaffected by the quantization.
Figure 4(a) compares accuracy as function of referral rate. It shows that BNN and QBNN achieve 99.5% accuracy by referring only 6% and 8.5% of samples to a domain expert, respectively, whereas the standard ResNet-50 has a 27.5% referral rate. This indicates that false negatives and false positives can be eradicated with fewer data referrals to a domain expert, a 78% improvement in referral rate efficiency with QBNN compared to DNN.
We use the Camelyon17-wilds dataset to test the model for OOD detection. This dataset comprises 450,000 patches extracted from 50 whole-slide images of breast cancer metastases in lymph node sections. We use 1,000 randomly selected images from the validation set to the test models for OOD detection. OOD detection is a binary classification task to identify whether the data sample belongs to in-distribution data. We evaluate the ability of the model to detect OOD data using predictive uncertainty estimates, which is an unsupervised approach (i.e., the model has no knowledge of OOD data). Figure 4(b) shows the comparison of area under the receiver operating characteristic curve (AUC) for OOD detection. BNN (AUC of 0.83) shows superior ability to detect OOD samples compared to DNN (AUC of 0.41). Furthermore, the quantization of BNN has little effect on the OOD detection AUC.
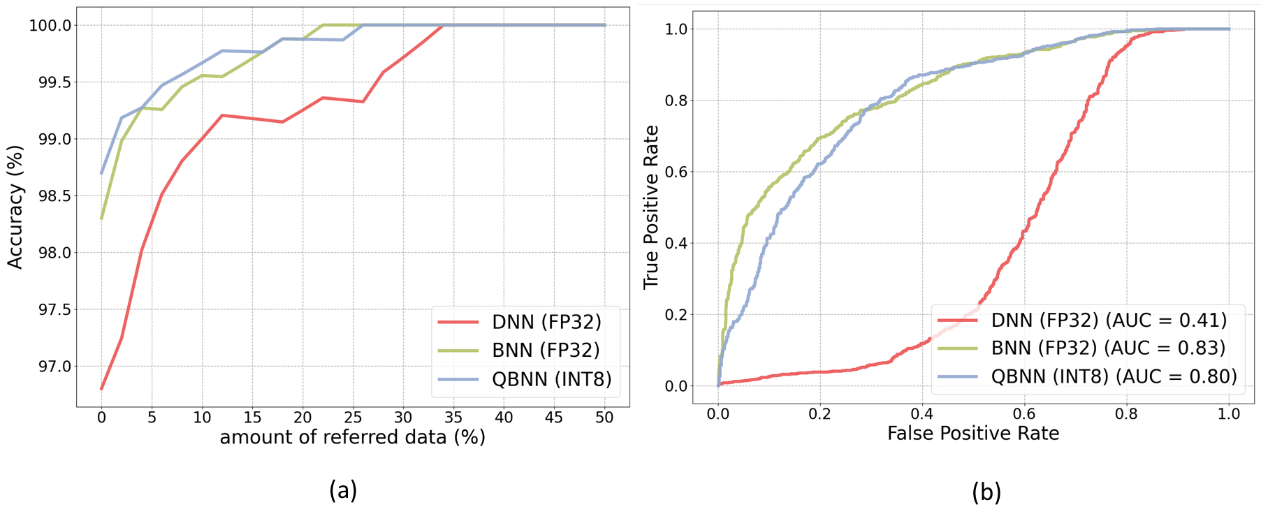
Figure 4. Accuracy as a function of amount of data referred based on predictive uncertainty
Concluding Remarks
We presented a low-precision optimization framework for Bayesian deep learning that enables post-training quantization of BNNs using simple and familiar APIs. With the Bayesian-Torch quantization framework, the optimized 8-bit integer (INT8) BNN achieved up to 6.9x inference throughput speedup (Figure 5) and required 4x less memory compared to 32-bit floating-point (FP32) BNN, without sacrificing the model accuracy, quality of uncertainty, and robustness properties. This was demonstrated through extensive empirical analysis on large-scale datasets and real-world applications. We have open-sourced the code for the quantization framework, and we envision this can enable wider deployments of Bayesian deep learning models in practical applications.
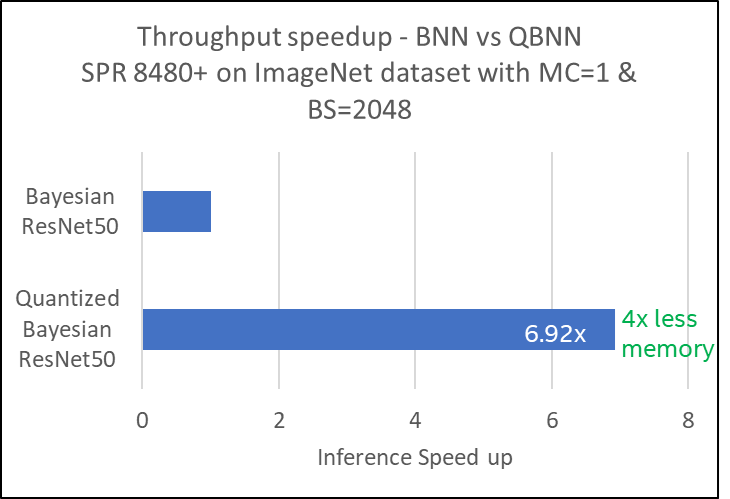
Figure 5. Throughput speedup comparison of BNN vs QBNN
