Contributors:
Bao, Jiulong: jiulong.bao@intel.com
Zhang, Yu: yu.d.zhang@intel.com
Wang, Yang: yang.y.wang@intel.com
Du, Jessica: jessica.du@intel.com
Abstract
PCL (Point Cloud Library) has widely been used in various scenarios, but due to the huge amount of point cloud data, the performance requirements are getting higher and higher. In this article, we have used Intel® Advanced Vector Extensions 512 (Intel® AVX-512) intrinsic instructions and Intel® Threading Building Blocks (Intel® TBB) multithreading method on the 11th Generation Intel® Core™ i7 processors (formerly known as Tiger Lake) platform to optimize the PCL plane segmentation algorithm (Plane Segmentation) and clustering algorithm (Object Clustering), so that the performance can be improved to 10%-300 %.
Introduction
Point Cloud and PCL Library Introduction
A point cloud is a set of data points in space. The points may represent a 3D shape or object. Each point position has its set of Cartesian coordinates (X, Y, Z). Point clouds are generally produced by 3D scanners or by photogrammetry software, which measure many points on the external surfaces of objects around them. As the output of 3D scanning processes, point clouds are used for many purposes, including creation of 3D CAD models for manufactured parts, for metrology and quality inspection, and for a multitude of visualization, animation, rendering and mass customization applications1.
The Point Cloud Library (PCL) is an open-source library of algorithms for point cloud processing tasks and 3D geometry processing, as occurs in three-dimensional computer vision. The library contains algorithms for segmentation, filtering, feature estimation, etc. Each module is implemented as a smaller library that can be compiled separately. The modularity of the PCL makes the algorithm realization process more compact and clear. And it also facilitates the customization and optimization of specific PCL algorithms.
Hardware and Software Configuration with the 11th Generation Intel® Core™ i7 processors (formerly known as Tiger Lake) Processory
All our test results presented in this document, are collected from below platform:
Intel® Core™ i7-1185GRE processor (detailed specs see below2 )
| Platform | i7-1185GRE |
|---|---|
| Core Processor | Intel® Core™ i7-1185GRE, 4 core @ 2.80 GHz No Turbo |
| iGPU | Intel® Iris® Xᵉ graphics, 96EU, up to 1.35 GHz |
| Memory | LPDDR4 8G, speed: 4267 MT/s |
| Bios Vendor | Intel Corporation |
| Bios Version | TGLSFWI1.R00.4024.A01.2101201730 |
| Operating System | Ubuntu* 20.04.1 LTS |
| Linux* Kernel | 5.8.0-50-generic |
| PCL Version | 1.11 |
| FLANN Version | 1.90 |
| GCC Version | 11.3 |
| Test Date | 2021/07/21 |
PCL Optimization Solutions
Plane Segmentation Algorithm Optimization
In the PCL library, the ground segmentation feature is implemented using the RANSAC algorithm. RANSAC is the abbreviation of "RANdom SAmple Consensus". The input of the RANSAC algorithm is a set of observed data, a parameterized model used to interpret the observed data, and some credible parameters. RANSAC uses an iterative method to estimate parameters of a plane model from a subset of observed data. The selected subset is assumed to be an inlier point, and the following method is used to verify:
- There is a model adapted to the hypothetical interior point, that is, all unknown parameters can be calculated from the hypothetical inlier point.
- Use the model which is got from the step above to test all other data. If the point is applicable to the estimated model, assume it as an inlier point.
- If enough points are classified as hypothetical inlier points, then the estimated model is accepted.
- Then, use all the assumed inlier points to re-estimate the model (for example, using the least squares method), because it has only been estimated by the initial assumed interior points.
- Finally, the model is evaluated by the error rate of the inlier points and the model.
- The above process is iterated many times, and the model is either discarded because there are too few interior points or selected because it is better than the existing model.
The RANSAC algorithm is a data-intensive calculation that can be optimized using SIMD (Single Instruction Multiple Data) vectorized instructions. SIMD instructions can process data from multiple data sets in a CPU cycle, which can greatly improve the data throughput and execution efficiency. SIMD is applicable to a wide range of platforms, from MMX™ Technology, Intel® Streaming SIMD Extensions (Intel® SSE), Intel® Advanced Vector Extensions (Intel® AVX), to Intel® Advanced Vector Extensions 2 (Intel® AVX2), which can be used on multi-generation x86 platforms, and 512-bit wide instruction set Intel® AVX-512, Intel® AVX-512 instructions have been supported on the latest 11th Generation Intel® Core™ i7 processors.
In the latest version of PCL1.11 3, the calculation of the distance between the point and the plane has been implemented by Intel® AVX2 in the RANSAC algorithm, it has greatly improved performance compared to the C++ language implementation. As the latest generation of the 11th Generation Intel® Core™ i7 processors (formerly known as Tiger Lake) already supports Intel® AVX-512. RANSAC is implemented using Intel® AVX-512 instructions to further enhance data parallelism. The key function is implemented as follows.

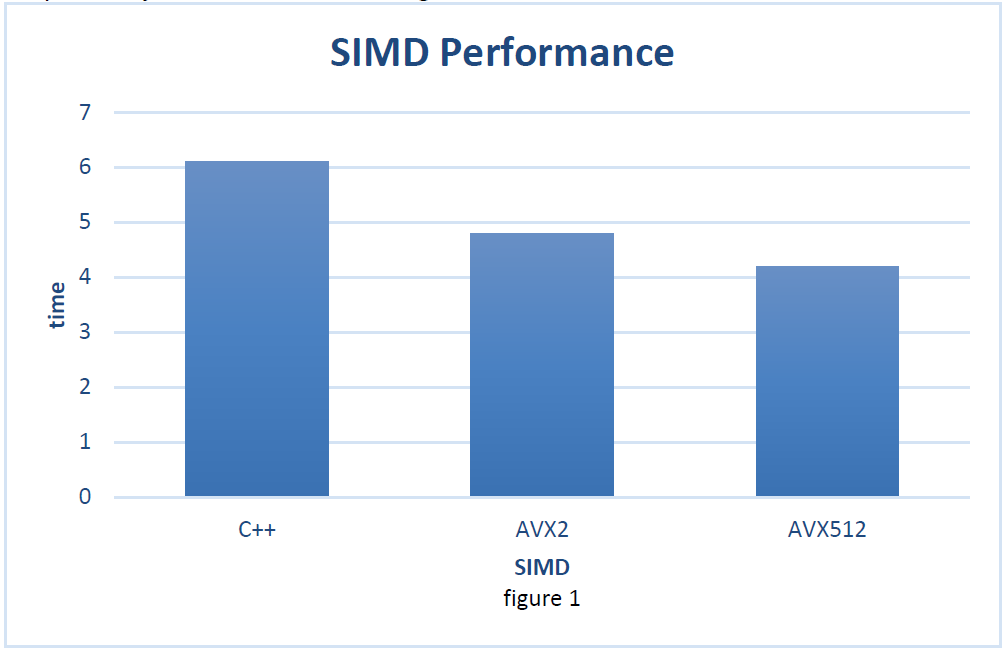
The following is a comparison of the time cost of plane segmentation running on cloud point data which contains 120000 points. By comparing the implementation of C++ and Intel® AVX2, the Intel® AVX-512 implementation has improved performance by 10-30%, respectively. The results are as Figure 1.
Euclidean Clustering Algorithm Optimization
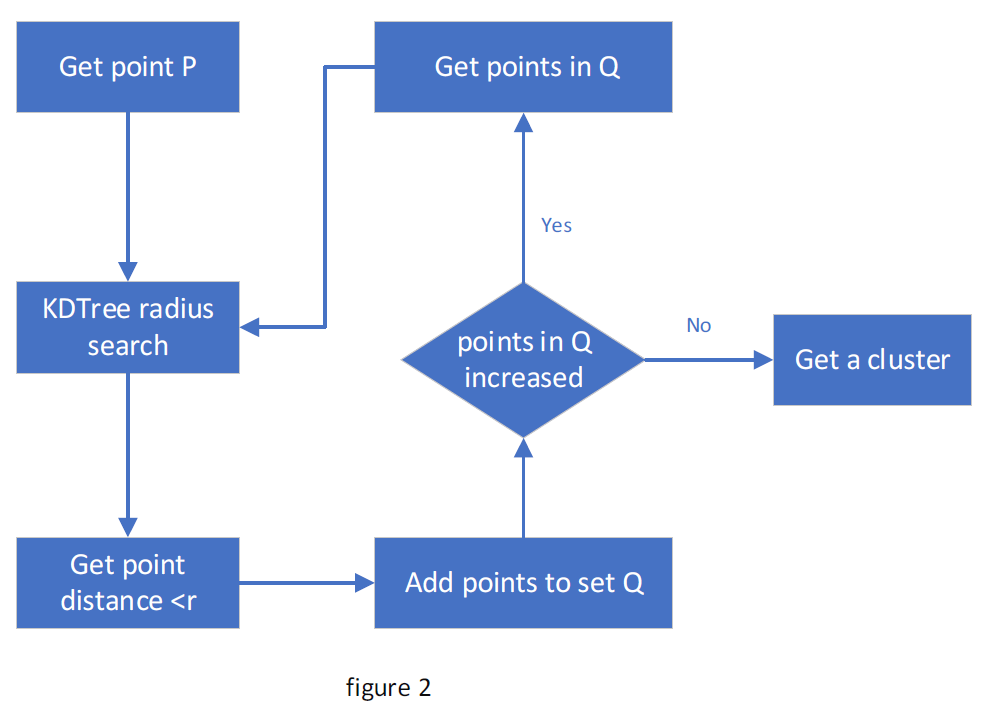
Euclidean clustering is a clustering algorithm based on Euclidean distance, and the radius search algorithm based on KD-Tree is an important preprocessing method to accelerate Euclidean clustering. The principle of the algorithm is that, given a certain point P in space, the KD-Tree radius search algorithm that is used to find the points which distance from the point P is less than r, and add them into the set Q. If the number of elements in Q doesn’t increase, the entire clustering process ends; otherwise, select points other than point P in the set Q and repeat the above process until the number of elements in Q no longer increases. In PCL, the Euclidean clustering process flow is shown in Figure 2.
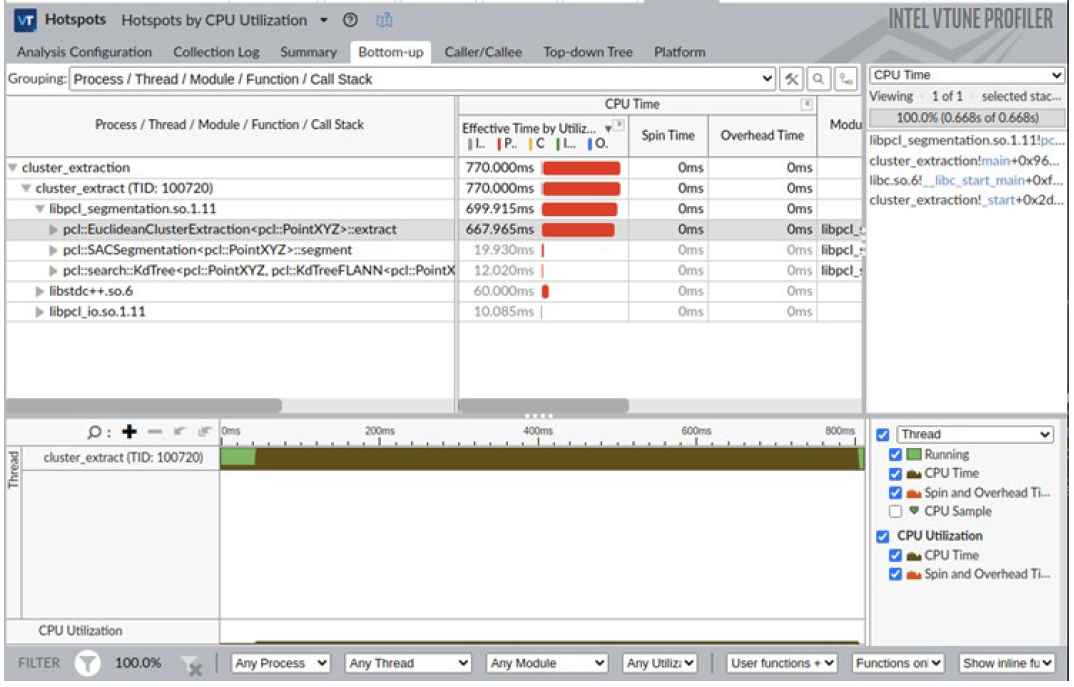
We used the VTune™ tool from Intel® oneAPI Base Toolkit (Base Kit) to analyze the performance bottleneck of the Euclidean clustering algorithm. The performance status is shown in Figure 3. It can be concluded from the performance analysis of VTune that the time of the Euclidean clustering algorithm is mainly spent on the Kd-Tree radius search
According to flow shown in Figure 2 of Euclidean clustering algorithm, we know that the selection of point P has randomness and uncertainty, but the points in the set Q obtained by Kd-Tree radius search are related and belong to the same cluster. Therefore, using multithread to select the points in the set Q for Kd-Tree radius searching can greatly improve the speed of Euclidean clustering without increasing the complexity. The process of the clustering algorithm using multithread is shown in Figure 4.
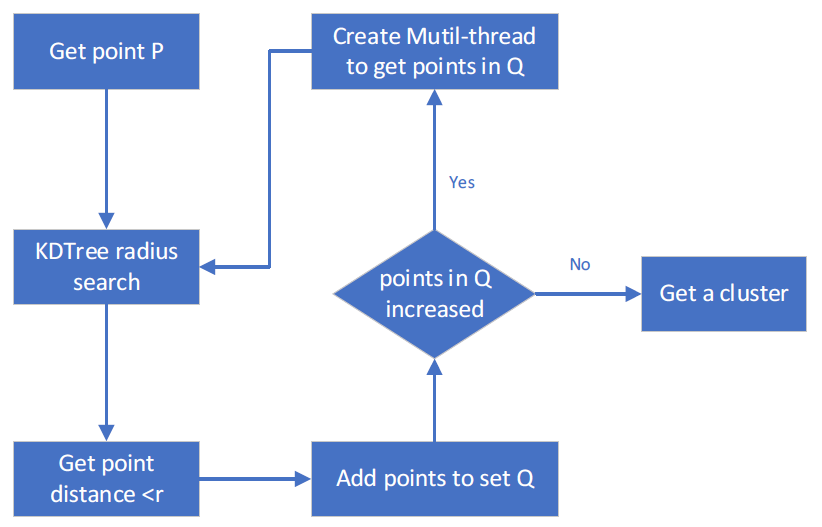
According to Figure 4, the Intel® TBB multi-threading solution for Euclidean clustering as follows:
- Get point P,
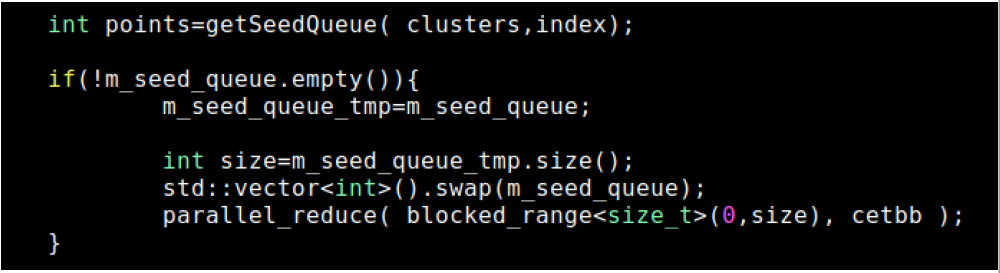
- Intel® TBB multi-threading to Kd-Tree radius search
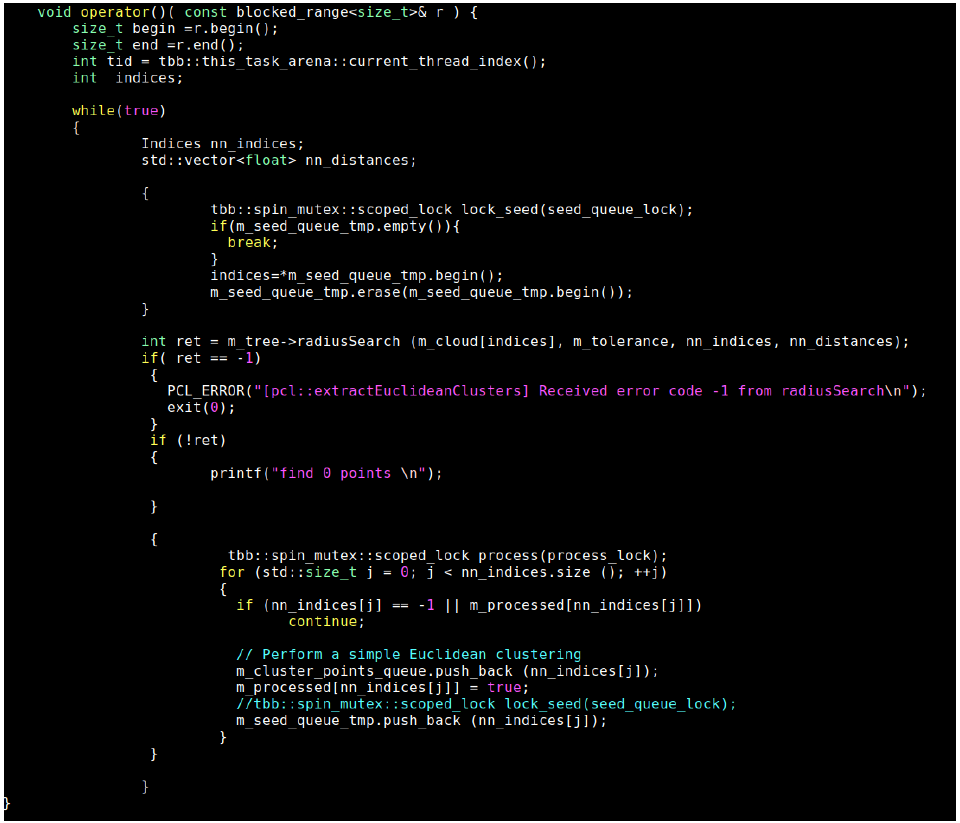
Using the multi-threading Euclidean clustering algorithm, the performance improvement effect is different in the point cloud size. The test results are shown in Figure 5.
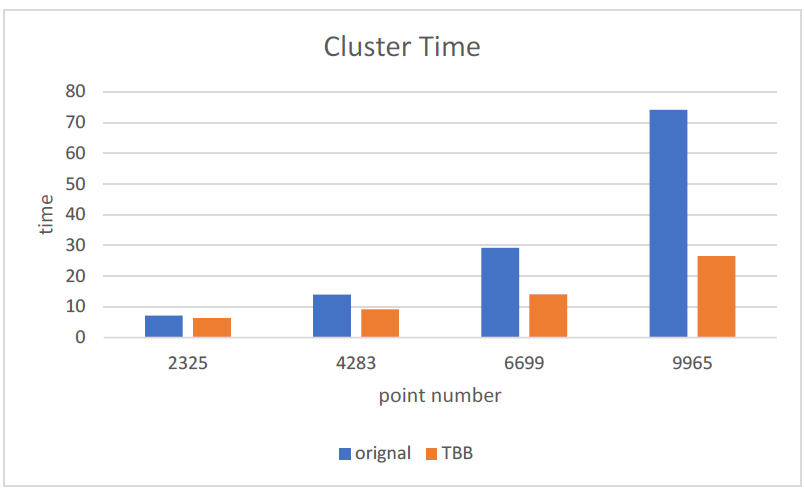
From the test results, it can be seen when the number of point cloud points is 6,500, the performance of the Intel® TBB multi-threading Euclidean clustering is doubled compared with the original scheme. And the point cloud points number reaches 10,000 points, and the processing speed is about 2 times faster. Based on the test results, it is recommended to use this multi-threading algorithm when the number of points exceeds 5000.
Inclusion
Many PCL use scenarios are based on the processing of massive point cloud data. SIMD instructions and multithreading methods provide effective solutions for PCL optimization. However, there are still many algorithms in the PCL library. Using SIMD instructions and multithreading, optimizing the performance of these algorithms one by one is also a long-term work for us, and will be further discussed in the future.