The Strided API for the Intel® oneAPI Math Kernel Library Vector Math Component

Introduction

This article discusses the Strided API, a functionality in Intel® oneAPI Math Kernel Library (oneMKL), which was introduced in the Vector Math (VM) component, version 2020.

This functionality allows you to use non-unit increments when traversing input and output arrays of a VM mathematical function. It is particularly useful in multidimensional array processing, which is widely demanded in the popular NumPy package for Python*. The VM API allows it to be done in just one pass in parallel mode.

Description

Originally the VM component of oneMKL was designed to support simple one-dimensional arrays processed by unit index increments. But in some cases, only selected elements of an input array with some fixed steps need to be processed and written to an output array using some other fixed steps.

In this article, we show how a one-dimensional VM approach can be extended to a multidimensional case and support the NumPy notion of strides. NumPy strides are the number of bytes to jump over in memory in order to get from one item to the next along each direction and dimension of the array. It is the separation between consecutive items for each dimension. With NumPy strides, Python users can process multidimensional arrays with complex layouts in any direction, such as vertical and horizontal, using arbitrary increments.

Emulate with Threaded Loops

The VM component is used in the NumPy package for performance optimization. The lack of a strided interface for VM mathematical functions in previous oneMKL releases can be emulated by simple threaded loops before and after the VM call. For example:

#pragma omp parallel for
for(i=0;i<n;i++){ packed_input[i] = input[i*inca]; } 
vdExp(n, packed_input, packed_result);
#pragma omp parallel for
for(i=0;i<n;i++){ result[i*incr] = packed_result [i]; }

Emulate with Functions

You can also emulate a strided interface by calling special VM pack and unpack functions:

vdPackI (n, input, inca, packed_input);
vdExp (n, packed_input, packed_result);
vdUnpackI (n, packed_result, result, incr);

There are several obvious drawbacks to these emulation approaches:

• Additional memory consumption for intermediate packed arrays.
• Three passes through memory rather than one (possible performance loss).
• Threads creation overhead for three sections rather than one (more performance loss, mostly on shorter vector lengths).

Combined Functions with a Computational Core

The new strided API combines pack and unpack functions with a computational core. It does so within the same pass-through memory and the same parallel section (in the case of a threaded layer). The difference with a classic interface is additional increment parameters after each array and the I suffix in the function name:

vdExpI (n, input, inca, result, incr);

The pseudo-code for the previous example is as follows:

vdExpI (n, input, inca, result, incr)
{
   for(i=0; i < n; i++)  
   {
        result[i*incr] = exp( input[i*inca] );
   }
}

All previously available functionality is also supported in the new strided API:

• Full VM functions list
• All precisions (single, double, complex)
• Accuracies (VML_HA, VML_LA, VML_EP)
• Computation
• Error-handling modes

In-place operations are also supported, but only when the corresponding input and output increments are equal.

Increment values for each input and output array can be different in general.

Notes

• For NumPy developers, strided VM increment parameters are measured in elements of a corresponding data type while NumPy stride units are measured in bytes–a conversion may be required.
• n is the number of elements to be processed, not the maximum array size. So, when calling vdExpI (n, input, inca, result, incr), be sure that the input vector is allocated for at least 1 + (n-1)*inca elements and the result vector has a space for 1 + (n-1)*incr elements.

Example

The following example shows how to implement the NumPy np.Add function through a strided VM call:

np.add(A, B):
for (i0, i2) in zip(range(0, 2), range(0, 2)):
 for i1 in range(3):
 C[i0, i1, i2] = A[i0, i1, i2] + B[i0, i1, i2]

It can be expressed as:

for(i0=0 ; i0 < 2; ++i0) 
{
 for(i2=0 ; i2 < 2; ++i2) 
 {
 DOUBLE_add({&A[i0,0,i2], &B[i0,0,i2], &C[i0,0,i2]}, {3,3,3}, {2,2,2}) 
 }
}

DOUBLE_add({ &p0, &p1, &p2 }, {n, n, n}, {st0, st1, st2})
{
 for (i=0; i<n; i++, p0+=st0, p1+= s1, p2+=st2)
 {
 double v0 = *((double *) p0), 
 double v1 = *((double *) p1);
 double u = v0 + v1;
 *((double *)p2)= u;
 }
}

If the strides were equal to 1, we could have called vdAdd.

In the following example, stride=2, so the new strided vdAddI is needed:

DOUBLE_add({ &p0, &p1, &p2 }, {n, n, n}, {st0, st1, st2})
{
 vdAddI(n, p0, st0, p1, st1, p2, st2);
}

Performance Comparison

This performance comparison is based on a simple CPU timestamp counter and provides clock cycles per element (CPE) values. The new strided VM vdExpI HA (high accuracy) function performance was compared to the simple "packed" emulation approach that is implemented through threaded loops. For details, see Emulate with Threaded Loops.

Input arguments are uniformly distributed in the interval [-10.0, 10.0].

Performance by stride sizes (3, 7, 11, 33, 66, and 123) with a fixed vector length of 1,000,000 are shown in Figure 1:
[1.8]

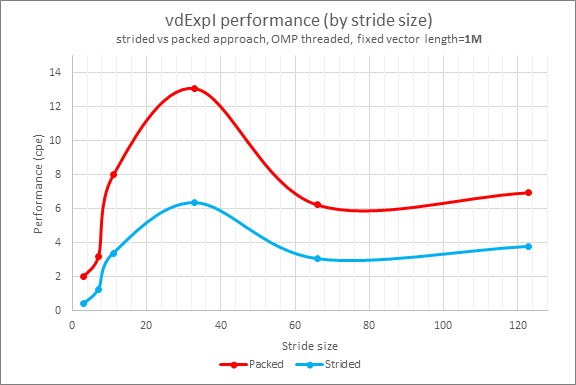
Figure 1

Performance by vector lengths (10 K, 50 K, 100 K, 500 K, 1 M, and 5 M) with a fixed stride size of 33 are shown in Figure 2:

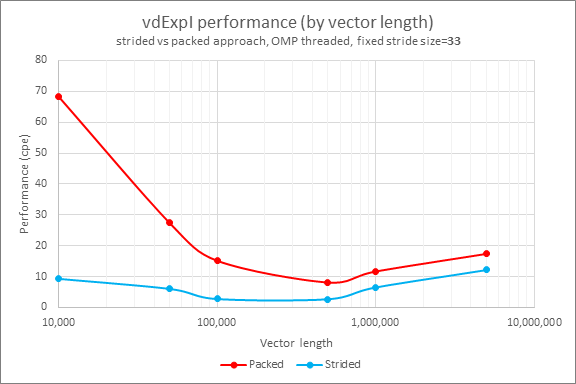
Figure 2

The new strided VM API demonstrates 1.4x to 7.3x performance benefits and reduces memory consumption in comparison to the approach in Emulate with Threaded Loops.

Environment

The following resources were used:

Hardware: 2nd generation Intel® Xeon® Scalable processors, (formerly code named Cascade Lake), 128 GB memory, 2 sockets, 24 cores per socket, cache size: L1: 32 KB plus 32 KB, L2: 1 MB, L3: 36 MB, hyper threading and throttling are off.

Software:
• Red Hat Enterprise Linux* 7.2
• oneMKL code is linked with the Threading Building Blocks layer in oneMKL.