Intel® Math Kernel Library - Introducing Vectorized Compact Routines

Introduction     

    Many high performance computing applications depend on matrix operations performed on large groups of matrices of small sizes. Intel® Math Kernel Library (Intel® MKL) 2018 and later versions provide new compact routines that include optimizations for problems of this type.

The main idea behind these compact routines is to create true SIMD computations, in which subgroups of matrices are operated on with kernels that abstractly appear as scalar kernels while registers are filled by cross-matrix vectorization. Intel MKL compact routines provide significant performance benefits compared to batched techniques (see /content/www/us/en/develop/articles/introducing-batch-gemm-operations.html for more detailed information about Intel MKL Batch functions), while maintaining ease-of-use through the inclusion of compact service functions that facilitate the reformatting of matrix data for use in these routines.

Compact routines operate on matrices that have been packed into a contiguous segment of memory in an interleaved format, called compact format. Six compact routines have been introduced in Intel MKL 2018: general matrix-multiply (mkl_?gemm_compact), triangular matrix equation solve (mkl_?trsm_compact), inverse calculation (mkl_?getrinp_compact), LU factorization (mkl_?getrfnp_compact), Cholesky decomposition (mkl_?potrf_compact), and QR decomposition (mkl_?geqrf_compact). These routines can only be used for groups of matrices of identical dimensions, where the layout (row-major or column-major) and the stride are identical throughout the group. 

Compact Format

    In compact format, for real precisions, matrices are organized into packs of size V, where V is related to the SIMD vector length of the underlying architecture. Each pack is a 3D tensor with the matrix index incrementing the fastest. These packs can then be loaded into registers and operated on using SIMD instructions.

The picture below demonstrates the packing of a set of 4, 3 x 3, real-precision matrices into compact format. The pack length for this example is V = 2, resulting in 2 compact packs.

   Figure 1: Compact format for 4, 3 x 3, real precision matrices with pack length V = 2

The particular form for the packs for each architecture and problem precision are specified by a MKL_COMPACT_PACK enum type.

Before calling a BLAS or LAPACK compact function, the input data must be packed in compact format. After execution, the output data should be unpacked from this compact format, unless another compact routine will be called immediately following the first. Two service functions, mkl_?gepack_compact, and mkl_?geunpack_compact, facilitate the process of storing matrices in compact format. It is recommended that the user call these service functions before calling the mkl_?gepack_compact routine to obtain the optimal format for performance, but advanced users can pack and unpack the matrices themselves and still use Intel MKL compact kernels on the packed set.

For more details, including a description of the compact format of complex-type arrays, see <Compact Format> in the Intel MKL User’s guide.

A SIMPLE VISUAL EXAMPLE

A simple compact version of a matrix multiplication is illustrated in this section, performing the operation C = A * B for a set of 4, 3 x 3, real-precision matrices. Generic (or batched) routines require 4 matrix-matrix multiplications to be performed for a problem of this type, as illustrated in Figure 2.

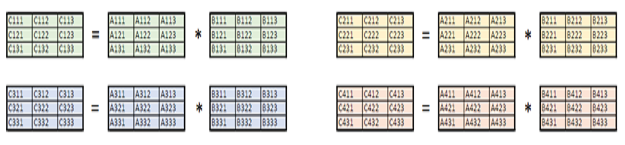
                               Figure 2: Generic GEMM for a set of 4, 3 x 3 matrices

Assuming that the matrices have been packed into compact format using a pack length of V = 2, the compact version of this problem involves two matrix-matrix multiplications, as illustrated in Figure 3

                                Figure 3: Compact GEMM for a set of 4, 3 x 3 matrices

The elements of the matrices involved in these two multiplications are vectors of length V, which are loaded into registers and operated on as if they were a scalar element in an ordinary matrix-matrix multiplication. Clearly, it is optimal to have pack length V equal to the length of the SIMD registers of the architecture.

NUMERICAL LIMITATIONS

Compact routines are subject to a set of numerical limitations, and they skip most of the checks presented in regular BLAS and LAPACK routines to provide effective vectorization. Error checking is the responsibility of the user. For more information on limitations in compact routines, see <MKL User Guide Numerical Limitations>

BLAS COMPACT ROUTINES

Intel MKL BLAS provides compact routines for general matrix-matrix multiplication and solving triangular matrix equations. The following table provides a brief description of the new routines. For detailed information on usage for these routines, see the Intel MKL User’s Guide.

LAPACK COMPACT ROUTINES

Intel MKL LAPACK provides compact functions to calculate QR, LU, and Cholesky decompositions, as well as inverses, in Intel MKL 2018 (and later versions). The compact routines for LAPACK follow the same optimization principles as the compact BLAS routines. The following table provides a brief description of the new routines. For detailed information on these routines, see the Intel MKL User’s Guide.

Example

The following example uses Intel MKL compact routines to calculate first the LU factorizations, then the inverses (from the LU factorizations), of a group of 2048, 8x8 matrices. Within this example, the same calculations are made using an OpenMP loop on the group of matrices. The time that each routine takes is printed so that the user can verify the performance improvement when using compact routines.

Notice that the routines mkl_dgetrfnp_compact and mkl_dgetrinp_compact are called between the mkl_dgepack_compact and mkl_dgeunpack functions. Because the mkl_?gepack_compact and mkl_?geunpack_compact functions add overhead, users who call multiple compact routines on the same group of matrices will see the greatest performance benefit from using compact routines.

The complex compact routines are executed similarly, but it is important to note that for complex precisions, all input parameters are of real type. For more details, see <Compact Format> in the Intel MKL User’s guide. Examples of the calling sequences for each individual routine can be found in the Intel MKL 2018 product.

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include "mkl.h"

#define N                        8
#define NMAT                  2048

#define NITER_WARMUP            10

void test(double *t_compact, double *t_omp) {
    MKL_INT i, j;

    MKL_LAYOUT layout = MKL_COL_MAJOR;
    MKL_INT m = N;
    MKL_INT n = N;
    MKL_INT lda = m;

    MKL_INT info;
    MKL_COMPACT_PACK format;
    MKL_INT nmat = NMAT;

    /* Set up standard arrays in P2P (pointer-to-pointer) format */
    MKL_INT a_size = lda * n;
    MKL_INT na = a_size * nmat;
    double *a_ref = (double *)mkl_malloc(na * nmat * sizeof(double), 128);
    double *a = (double *)mkl_malloc(na * nmat * sizeof(double), 128);
    double *a_array[NMAT];
    double *a_compact;

    /* For random generation of matrices */
    MKL_INT idist = 1;
    MKL_INT iseed[] = { 0, 1, 2, 3 };
    double diag_offset = (double)n;

    /* For workspace calculation */
    MKL_INT imone = -1;
    MKL_INT lwork;
    double work_query[1];
    double *work_compact;

    /* For threading */
    MKL_INT nthr = omp_get_max_threads();
    MKL_INT ithr;
    MKL_INT lwork_i;
    double *work_omp;
    double* work_i = work_omp;

    /* For setting up compact arrays */
    MKL_INT a_buffer_size;
    MKL_INT ldap = lda;
    MKL_INT sdap = n;

    /* Random generation of matrices */
    dlarnv(&idist, iseed, &na, a);

    for (i = 0; i < nmat; i++) {
        /* Make matrix diagonal dominant to avoid accuracy issues
                 in the non-pivoted LU factorization */
        for (j = 0; j < m; j++) {
            a[i * a_size + j + j * lda] += diag_offset;
        }
        a_array[i] = &a[i * a_size];
    }
    /* Set up a_ref to use in OMP version */
    for (i = 0; i < na; i++) {
        a_ref[i] = a[i];
    }

    /* -----Start Compact----- */

    /* Set up Compact arrays */
    format = mkl_get_format_compact();

    a_buffer_size = mkl_dget_size_compact(ldap, sdap, format, nmat);

    a_compact = (double *)mkl_malloc(a_buffer_size, 128);

    /* Workspace query */
    mkl_dgetrinp_compact(layout, n, a_compact, ldap, work_query, imone, &info, format, nmat);
    lwork = (MKL_INT)work_query[0];
    work_compact = (double *)mkl_malloc(sizeof(double) * lwork, 128);

    /* Start timing compact */
    *t_compact = dsecnd();

    /* Pack from P2P to Compact format */
    mkl_dgepack_compact(layout, n, n, a_array, lda, a_compact, ldap, format, nmat);

    /* Perform Compact LU Factorization */
    mkl_dgetrfnp_compact(layout, n, n, a_compact, ldap, &info, format, nmat);

    /* Perform Compact Inverse Calculation */
    mkl_dgetrinp_compact(layout, n, a_compact, ldap, work_compact, lwork, &info, format, nmat);

    /* Unpack from Compact to P2P format */
    mkl_dgeunpack_compact(layout, n, n, a_array, lda, a_compact, ldap, format, nmat);

    /* End timing compact */
    *t_compact = dsecnd() - *t_compact;
    /* -----End Compact----- */

    /* -----Start OMP----- */
    for (i = 0; i < nmat; i++) {
        a_array[i] = &a_ref[i * a_size];
    }

    /* Workspace query */
    mkl_dgetrinp(&n, a_array[0], &lda, work_query, &imone, &info);
    lwork = (MKL_INT)work_query[0] * nthr;
    work_omp = (double *)mkl_malloc(sizeof(double) * lwork, 128);

    /* Start timing OMP */
    *t_omp = dsecnd();

    /* OpenMP loop */
    #pragma omp parallel for
    for (i = 0; i < nmat; i++) {
        /* Set up workspace for thread */
        ithr = omp_get_thread_num();
        lwork_i = lwork / nthr;
        work_i = &work_omp[ithr * lwork_i];

        /* Perform LU Factorization */
        mkl_dgetrfnp(&n, &n, a_array[i], &lda, &info);

        /* Perform Inverse Calculation */
        mkl_dgetrinp(&n, a_array[i], &lda, work_i, &lwork_i, &info);
    }

    /* End timing OMP */
    *t_omp = dsecnd() - *t_omp;
    /* -----End OMP----- */

    /* Deallocate arrays */
    mkl_free(a_compact);
    mkl_free(a);
    mkl_free(a_ref);
    mkl_free(work_compact);
    mkl_free(work_omp);
}

int main() {
    MKL_INT i = 0;
    double t_compact;
    double t_omp;
    double flops = NMAT * ((2.0 / 3.0 + 4.0 / 3.0) * N * N * N);
    for (i = 0; i < NITER_WARMUP; i++) {
        test(&t_compact, &t_omp);
    }
    test(&t_compact, &t_omp);
    printf("N = %d, NMAT = %d\n", N, NMAT);
    printf("Compact time = %fs, GFlops = %f\n", t_compact, flops / t_compact / 1e9);
    printf("OMP     time = %fs, GFlops = %f\n", t_omp,     flops / t_omp / 1e9);
    return 0;
}

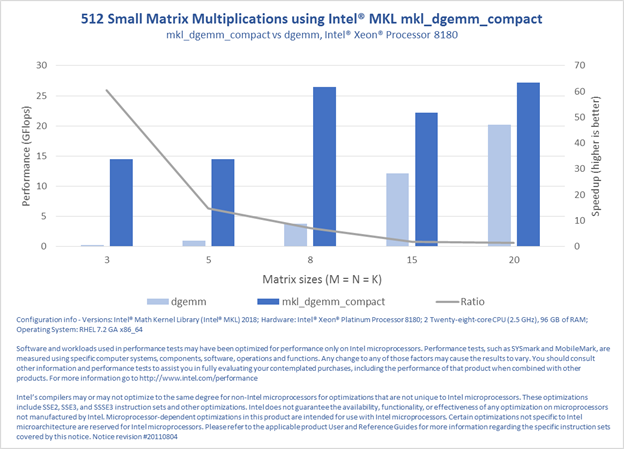
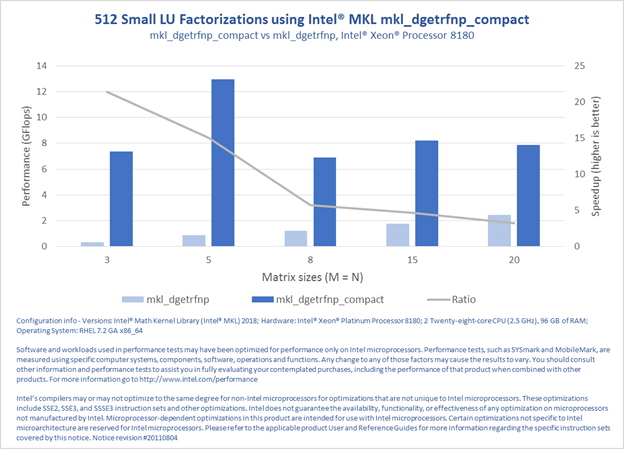
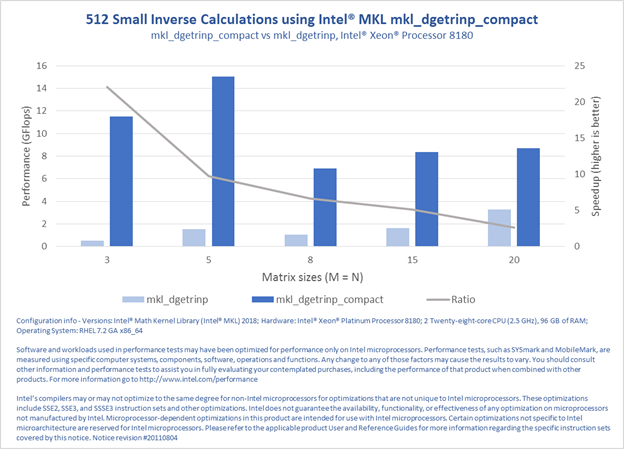
PERFORMANCE RESULTS

The following four charts demonstrate the performance improvement for the following operations: general matrix-matrix multiplication (GEMM), triangular matrix equation solve (TRSM), non-pivoting LU-factorization of a general matrix (GETRFNP), and inverse calculation of an LU-factorized (without pivoting) general matrix (GETRINP). The results were measured against calls to the generic BLAS and LAPACK functions, as in the above example.