Abstract
Checksums are widely used for checking the integrity of data in applications such as storage and networking. We present fast methods of computing checksums on Intel® processors. Instead of computing the checksum of the input with a traditional linear method, we describe a faster method to split the data into a number of interleaved parallel streams, compute the checksum on these segments in parallel, followed by a recombination step of computing the effective checksum using the partial checksums.
Introduction
Fletcher’s Checksum is a checksum that was designed to give an error detection capability close to that of a CRC, but with greatly improved performance (on general purpose processors).
It computes a number of sums, where C(0) is the sum of the input words, C(1) is the sum of the C(0) sums, etc. In general the sums are computed modulo M. In some cases M=2K, so high-order bits are just dropped. In other variants, M=2K-1.
ZFS is a popular file system originally designed by Sun Microsystems and open sourced. One of its features is protection against data corruption. For this purpose, it makes widespread use of either a Fletcher-based checksum, or a SHA-256 hash. The checksum has a much lower cost compared to a cryptographic hash function such as SHA-256, but is still significant enough to benefit from optimizations.
The variant of Fletcher that ZFS uses is based on having four sums (i.e., C(0)…C(3)), processing 32-bit chunks of input data (DWORDS), and computing the sums modulo 264.
While scalar implementations of Fletcher can achieve reasonable performance, this paper presents a way to further improve the performance by using the vector processing feature of Intel processors. The implementation was tailored to the particular Fletcher variant used in ZFS, but the same approach could be applied to other variants.
Implementation
If the input stream is considered to be an array of DWORDs (data) and the checksum consists of 4 QWORDS (A, B, C, D; initialized to 0), then the checksum can be defined as:
for (i=0; i<end; i++) {
A += data[i];
B += A;
C += B;
D += C;
}
When trying to speed this up, an obvious approach is to use the SIMD instructions and registers. But there are multiple ways to do this.
One approach is to divide the input buffer into 4 contiguous chunks (i.e., the first quarter, the second quarter, etc.), compute the checksum on each one separately, and then combine them. There are two problems with this approach. Unless the buffers are all of a fixed size, the way in which the partial results are combined will vary with each different buffer size. Furthermore, that first addition will require a gather operation to assemble the four input values, which adds extra overhead. This could be reduced by unrolling the loop, reading multiple DWORDS from each quarter, and then “transposing” the registers. Still, non-trivial overhead will be associated with reading the data.
The most efficient approach is to take the simple scalar loop and implement it in SIMD instructions, e.g.:
.sloop vpmovzxdq data, [buf] ; loads DWORD data into QWORD lanes add buf, 16 vpaddq a, a, data vpaddq b, b, a vpaddq c, c, b vpaddq d, d, c cmp buf, end jb .sloop
This effectively stripes the buffer, so that lane j computes a checksum on DWORDS (4 i + j). It has no extraneous overhead (e.g., trying to marshal the input data); however, you need to compute the actual checksum from these four partial checksums. Fortunately in this approach the calculation does not depend on the size of the input buffer.
If “a” is a DWORD pointer to the value of the “a” ymm register, etc., then the final checksum can be simply computed as:
A = a[0] + a[1] + a[2] + a[3];
B = - a[1] - 2*a[2] - 3*a[3]
+ 4*b[0] + 4*b[1] + 4*b[2] + 4*b[3];
C = a[2] + 3*a[3]
- 6*b[0] - 10*b[1] - 14*b[2] - 18*b[3]
+ 16*c[0] + 16*c[1] + 16*c[2] + 16*c[3];
D = - a[3]
+ 4*b[0] + 10*b[1] + 20*b[2] + 34*b[3]
- 48*c[0] - 64*c[1] - 80*c[2] - 96*c[3]
+ 64*d[0] + 64*d[1] + 64*d[2] + 64*d[3];
Justification
Let Fi be the checksum after processing i DWORDS.
Let the input stream be a series of DWORDS: x1, x2, x3, …
Then by unrolling the loop, you can see that the elements of F are just weighted sums of the input DWORDS:
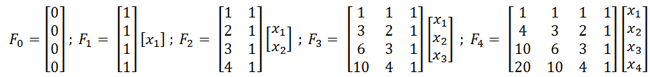
This is inconvenient, as the coefficients for X1 (for example) vary with the number of elements being considered. It is more convenient to renumber the input, so that y1 is the latest DWORD processed, y2 is the next most recent one, etc. That is, if we’ve processed n DWORDS, then yi = xn+1-i.
Then we find that
Or, in general
This is what we are trying to compute. But when we use the SIMD instructions, we are computing the checksums on every 4th DWORD. If we consider lane 3, which corresponds to y1, y5, etc., then we are actually computing:
And what we really want for that partial sum is (replacing i with (4i-3)):
If we compute the following weighted sums of the partial checksums:
It can be shown that (A”3 B”3 C”3 D”3) is the same as (A3 B3 C3 D3) and corresponds to the bolded (lane 3) terms in the recombination calculation shown in the previous section.
You can go through similar calculations for the other three lanes.
Performance
The performance results provided in this section were measured on an Intel® Core™ i7-4770 processor. The tests were run on a single core with Intel® Turbo Boost Technology off and with Intel® Hyper-Threading Technology (Intel® HT Technology) off and on1. The tests were run on a 16MB buffer that was warm in the cache, so that the cost of the recombination was insignificant.
The SIMD version described in this paper was compared against the best-known scalar implementation, which is the basic scalar implementation with the loop unrolled by a factor of 4. The results (in cycles/DWORD) were2:
| HT off | HT on | |
|---|---|---|
| Scalar | 1.62 | 1.56 |
| SIMD | 0.97 | 0.78 |
The performance of the simple scalar version is good, due to the super scalar nature of the processor. Since the processing for each DWORD requires four additions, this is operating at a rate of 2.5 additions per cycle (not including address updates or compares).
The Intel® Advanced Vector Extensions (Intel® AVX2) SIMD version runs at approximately 4 additions per cycle.
The SIMD version shows better scaling under Intel HT Technology, gaining approximately 24% in performance, as opposed to the scalar one, which only improved by 4%
The final merging operation does add some cycles, so for small buffers the scalar approach would be faster, but for large buffers, the SIMD approach can improve performance significantly. For processors that support Intel® Advanced Vector Extensions 512 (Intel® AVX-512), the vector width could be doubled to handle 8 parallel operations. This could approximately double the performance over the Intel AVX2 version for large data buffers.
Conclusion
This paper illustrates a method for improved checksum performance. By leveraging architectural features such as SIMD in the processors and combining innovative software techniques, large performance gains are possible.
Authors
Jim Guilford and Vinodh Gopal are architects in the Intel Data Center Group, specializing in software and hardware features relating to cryptography and compression.
Notes
1 Intel technologies may require enabled hardware, specific software, or services activation. Performance varies depending on system configuration. Check with your system manufacturer or retailer.
2 Software and workloads used in performance tests may have been optimized for performance only on Intel microprocessors. Performance tests, such as SYSmark* and MobileMark*, are measured using specific computer systems, components, software, operations and functions. Any change to any of those factors may cause the results to vary. You should consult other information and performance tests to assist you in fully evaluating your contemplated purchases, including the performance of that product when combined with other products.