Introduction
A few years ago I published this blog on the problem of the diminishing returns when adding more threads to a thread pool after you are already 8-10 cores wide. I focused on complexity and synchronisation in that document, and I didn’t dive much into Amdahl’s law to see what it says about performance scaling with high thread counts. Let’s have a quick look at that now.
Amdahl’s law – talking about P and n
Amdahl’s law is well-covered in literature as the basis for predicting the speedup S for a given code sample where:
P is a proportion of the code we can accelerate, and
n is the degree to which we can speed it up.
For simplicity I treat P as the proportion of code which can be threaded and n as the number of cores which will execute it. This is equivalent if the proportion of code P can be perfectly threaded.
\(Speedup = \frac{1} {1 - P + \frac{P}{n} }\)
It’s obvious in this form that as P trends towards zero, there is no benefit in increasing n. It’s also obvious that even as P trends toward 1, changing n from 2 to 4 makes a far bigger difference than changing it from 10 to 12. Slightly less obvious is that if n is infinite (Quantum Computer?), then P / n is zero, and the maximum scaling is now 1 / (1 – P). This suggests that with very high core counts like modern processors with 32 cores, it is important to focus on P, rather than n.
Shall we focus on P or on n? There is a third option: we can just remove some code from the critical path altogether by executing it on its own thread and – crucially – not have any critical path code stall while it waits for the removed code to finish. Work we typically consider background tasks like landscape generation, LOD or MIP streaming etc., are often written in this way. I’ve seen high-level NPC AI decision making code done this way, so the AI gets new goals every second or so. Audio is usually done this way too, since it doesn’t need to sync with the framerate of the game. With audio we trigger a sample, then a background thread ticks along at its own pace, keeping the circular buffer loaded when it needs to, regardless of the framerate of the game.
But why stop there? We can take almost any work we want and decouple it from the critical path, as long as we guarantee the decoupled work’s data is ready when the critical path code needs it.
Time to formalise the decoupling idea a bit…
Decoupled workload definition
A task which we trigger and leave to run on its own thread or group of threads until it’s done. Once it has finished, we take the data the task has created and swap it into the game, replacing the old data. For the task to be fully decoupled, the main thread of the game should never wait for the task to complete and ideally should be totally ignorant of the decoupled task’s current state. The decoupled task will typically build a new data set which the game will swap over to using once the task has finished. If Q is the proportion of code we can decouple, and it has the same proportion of threaded code in it as the rest of the game does, then Amdahl’s Law expands to:
\(Speedup = \frac{1}{ (1-Q) * (1-P+ \frac{P}{n} ) }\)
Using Decoupled Workloads
In a picture, the decoupled workload will work like this:

Fig. 1: Decoupled workload delivering a data set every 2 frames.
In this example, the decoupled work always finishes within two game frames, but we could theoretically make it as long as we want, so long as the CPU frame that the decoupled task supplies with data isn’t going to stall until the data is ready. Once the decoupled work has finished, it copies its results to the critical path at an appropriate moment – say end of frame. A trivial example could be an algorithm which determines whether a higher MIP for a texture is needed. If it is needed, then the algorithm can trigger a decoupled load to fetch the MIP from disk and continue using the old one in the meantime. Each frame, the algorithm can look to see if the new MIP is loaded, and once it is the algorithm can gradually introduce it.
This is not a new idea. As I previously mentioned, some games use this technique to change high level AI goals of groups of AI agents, but in those implementations the new data represents a sudden change of strategy and isn’t directly driving frame to frame changes. However, we can refine the idea of a decoupled workload quite a bit, to make it a much more powerful tool.
Refinement 1: Linear Interpolation
What if you have no linkage to game frames at all, and you trigger workloads on a timer? You could have a big task with a length just under 1/10th of a second and trigger that task every 1/10th of a second. The workload creates the data, then transfers it to the critical path code at the point where the next workload is triggered. That way you always have 2 data sets spaced 1/10th of a second apart, and the critical path code can derive its data by interpolating between the 2 data sets.
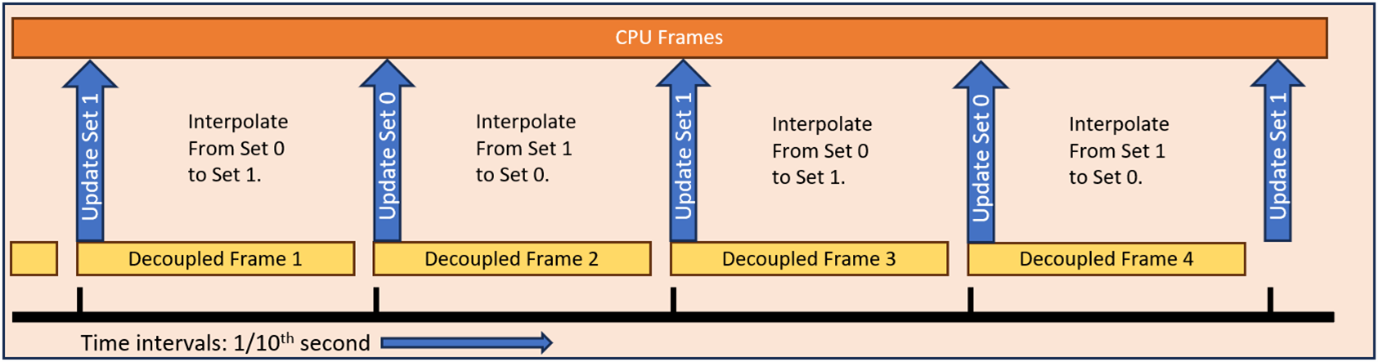
Fig. 2: Decoupled work triggering every 1/10th second and updating alternate data sets in the game.
In the Fig. 2. case, you can avoid any unnecessary copying by using an array of 3 data sets which you use as a circular buffer (there’s that audio thread again…). Initially, the game will interpolate between data set 0 and data set 1, while the decoupled task updates data set 2. After the decoupled workload finishes, we increment our pointers so we are now interpolating between data set 1, and data set 2, while the decoupled workload updates data set 0.
In a picture:

Fig. 3: Decoupled work triggering every 1/10th second and writing directly to data sets.
The table below shows how the two main threads in Hitman 3 by IO Interactive are scheduled mostly to the most performant cores without any affinity applied.
| Decoupled Frame | Data Set 0 | Data Set 1 | Data Set 2 |
|---|---|---|---|
| 0 | Start Value | End Value | Calculating |
| 1 | Calculating | Start Valu | End Value |
| 2 | End Value | Calculating | Start Valu |
| 3 | Start Valu | End Value | Calculating |
Table 1. Usage for each data set during each decoupled workload.
With this kind of setup, you could simulate something like a huge 3D vector field representing airflow or water movement. In Fig. 2., while the first decoupled frame is calculating Data Set 2, the game will interpolate between the flow vectors in Data Set 0, and the flow vectors in Data Set 1, using the elapsed time since the last 1/10th second tick. When the time reaches the 2nd 1/10th second marker, the first Decoupled Frame is finished, the next decoupled frame starts writing to Data Set 0, and the game can derive the flow vectors by using the time elapsed since the last 1/10th second tick to interpolate between Data Set 1 and Data Set 2.
Refinement 2: Non-Linear Interpolation using a Spline
The other big issue with the linear interpolation model above, is that if the changes from frame to frame are non-linear, say using accelerations etc., then you will not get a smooth set of values: the values will suddenly change directions at the end of each Frame creation. This might not be an issue for some kinds of data, but for the vector field example you need something smoother with no angles in it. A way around this is to increase the number of data sets to 5 and interpolate using a Catmull-Rom spline. There are many versions of this useful spline available on the Internet, including a lot of useful math and code here. The good thing about this spline is it passes through every control point, and (seldom) has any crazy sharp changes in direction.
The general idea is that at any moment in time we have 4 data sets in use, and the decoupled workload is writing to the fifth. We have a planned update period P which guaranteed to be longer than the longest the decoupled load is likely to take. Our interpolation value t is:
\(t = (𝐶𝑢𝑟𝑟𝑒𝑛𝑡 𝑇𝑖𝑚𝑒−𝐿𝑎𝑠𝑡 𝑈𝑝𝑑𝑎𝑡𝑒 𝑇𝑖𝑚𝑒) / 𝑃 \)
When t == 1 the decoupled workload is finished, so we
- increment our start pointer in the circular buffer.
- Set Last Update Time = Current Time.
- Trigger a decoupled workload to write to the data set after the one it previously updated.
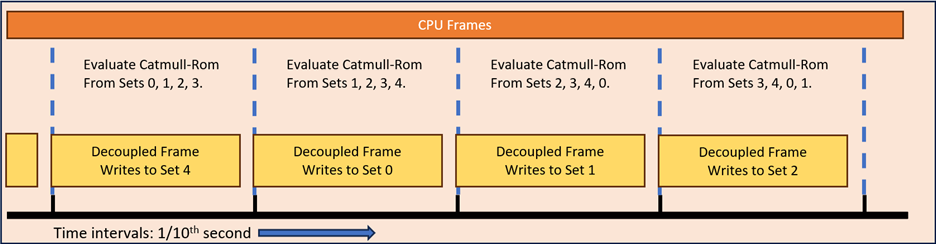
Fig. 4: Decoupled work triggering every 1/10th second and writing directly to data sets with Catmull-Rom spline interpolation.
Time to Talk About Time
You have probably noticed two key problems with this method with regards to time.
- All the data is in the past. In Fig. 3, we don’t get to the actual value generated by the decoupled work until 1/10th second later. In figure 4, we don’t get to the data until 2/10th second later. If your physics is time based this shouldn’t be much a problem for big tasks – you just add 2/10th second to the time which the decoupled work is using to generate its data. If your physics is incremental, then you need to think about predicting the location of actors which will affect the physics.
- You don’t get new data every frame, rather, each frame is an interpolation between some point in the past and the present. This is like a low-pass filter on the data so spikes in data which affect the decoupled work, and which are shorter than the period of the decoupled work, will not affect the output. But that’s not always a bad thing, right? It wouldn’t be the first time we have calculated exact data then blurred the result – that’s just ‘Graphics’, isn’t it?
Conclusions
In the previous article I was barking at the futility of chasing diminishing returns by adding more threads once your thread count is very large. Here I have presented here an argument for running more work asynchronously, and outlined one way to get some more flexibility from what is quite an old technique. In the race for optimized code, someone once pointed out that the fastest code is code that doesn’t actually run at all. As far as the critical path is concerned, decoupled work is exactly that.
Decoupling workloads in games presents a number of opportunities. Firstly, it is an optimisation technique where you escape the complexity of safely threading content on the critical path. Also, it enables the integration of code that might otherwise be impossible at the required framerate. Decoupling code from the critical path and running it independently will result in tangible framerate improvements if we do it right. Another benefit could be that decoupling helps hide sporadic CPU loads which are notorious for causing workload variations and uneven framerates.
Decoupling not only tackles technical obstacles but also represents an opportunity to free the developer to create complex systems to enhance games, without the worry of how it will impact the smooth display of the game's visuals. Such attention to detail could significantly enhance the realism of games, crafting a deeper and more immersive experience for gamers.
A Parting Segue – To the Future, and Beyond!
Lately I’ve been thinking about modern compute platforms from the point of view of imagining a good games programming model for a diverse collection of cores. We are likely to see this diversity in future hardware, and decoupling continues to look promising. For example, decoupling looks like a successful way to exploit the Efficient-cores in Intel’s latest range of hybrid CPUs, seamlessly hiding the occasional latency due to workload variations. Better still, if we think about the Neural Processing Unit (NPU) in Intel’s latest offering of Core Ultra, we would be able to construct far more complex and adaptable ML tools to enrich game content while not being constrained by a specific framerate. It seems to me that NPUs and decoupled programming models could lead to highly adaptable player driven gaming scenarios and graphical content.
We live in interesting times as the proverb goes, but rather than a curse we should embrace the opportunities available by marrying the right programming model to the right processor, developing and exploiting the massive range of possibilities the modern compute platform is opening for us, in the bold new future of heterogeneous computing!
Happy coding all.
Steve