
With multi-core processors now common place in PCs, and core counts continually climbing, software developers must adapt. By learning to tackle potential performance bottlenecks and issues with concurrency, engineers can future-proof their code to seamlessly handle additional cores as they are added to consumer systems.
To help with this effort, Intel software teams have created a graphics toolkit that shows how parallel processing techniques are best applied to eight different graphics filters. The entire source code package contains C++ files, header files, project files, filters, and database files. A DLL overlay with a simple user interface shows the speed at which each filter can be applied, both in a single-core system and when using parallel-processing techniques.
In this white paper, readers learn to use modern C++ techniques to process data in parallel, across cores. By studying the sample code, downloading the application, and learning the techniques, developers will better understand Intel® architecture and multi-core technology.
Getting Started with Parallel Processing
There are countless articles and books written on parallel processing techniques. Ian Foster has a good recap, and multiple papers have been presented at SIGGRAPH, including one by John Owens. A good reference is the 2015 book Programming Models for Parallel Computing, edited by Pavan Balaji. It covers a wide range of parallel programming models, starting with a description of the Message Passing Interface (MPI), the most common parallel programming model for distributed memory computing.
With applications across the computing spectrum, from database processing to image rendering, parallel processing is a key concept for developers to understand. Readers are assumed to have some experience and background in computer science to benefit from the concepts described here. The source code was written for C++, but the concepts extend to other languages, and will be of interest to anyone looking to better understand how to optimize their code for multi-core processors.
An in-depth discussion of the Intel architecture is beyond the scope of this article. Software developers should register at the Intel® Developer Zone and check out the documentation download page for Intel architecture to read some of the following manuals:
- Combined Volume Set of Intel® 64 and IA-32 Architectures Software Developer's Manuals
- Four-Volume Set of Intel® 64 and IA-32 Architectures Software Developer's Manuals
- Ten-Volume Set of Intel® 64 and IA-32 Architectures Software Developer's Manuals
- Software Optimization Reference Manual
- Uncore Performance Monitoring Reference Manuals
Getting Started
The system requirements to explore the Image Filters project solution are minimal. Any multi-core system with Windows® 10 is sufficient.
This project assumes that you have a C++ toolkit, such as Microsoft Visual Studio* with the .NET framework. Freebyte* has a full set of links here if you want to explore different C++ tools. To simply look through code, you may want to use a free code viewer such as NotePad++* or a similar product.
To begin exploring the Image Filters project, follow these steps:
- Create an empty directory on your computer with a unique title such as "Image Filters Project" or "Intel C++ DLL Project".
Use whatever naming strategy you are comfortable with; you can include the year, for example. - Download the .zip file to your new directory.
The file is not large—about 40 KB. After extracting the files and building the project, you will consume about 65 MB of disk space. - Extract the files in the new directory.
For example, if using 7-Zip*, right-click on the .zip file and select 7-Zip > Extract here. You can use any file compression software, such as 7-Zip, WinZip*, or WinRAR*. - Open Microsoft Visual Studio or similar C++ tool. These instructions assume that you loaded the most current version of Microsoft Visual Studio.
- Open the project by using File > Open > Project/Solution and locating the ImageFilters.sln file.
The ImageFilters.sln file should appear in the Solution Explorer on the left.
The ImageFilters solution has two projects:
a) ImageFiltersWPF — The client application that utilizes the ImageProcessing DLL and shows how to interact with it using C#.
b) ImageProcessing — The C++ DLL that contains the multi-core image processing algorithms.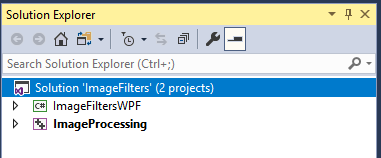
Figure 1. You must build both projects inside the Solution Explorer. - From the Solution Explorer, select the ImageFiltersWPF project; then hold down the CTRL key and select the ImageProcessing project.
- Right-click on one of the highlighted files to pull up an Actions menu and select Build Selection. This starts the compiler for both.
- Wait while the system quickly compiles the existing source files into the binary, .DLL, and .EXE files.
The following files display in the project solutions bin directory:
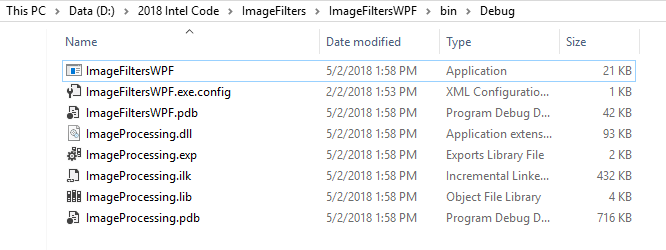
Figure 2. Compiled files in the bin > debug folder, including the ImageFiltersWPF executable.
Multithreading Technique
By default, applications run on a single processing core of a system. Because all new computing systems feature a CPU with multiple cores and threads, this implies that some complex calculations could be distributed intelligently, greatly speeding computation times.
OpenMP*(Open Multi-Processing) is an API first published in 1981 for Fortran 1.0 that supports multiplatform shared memory multiprocessing programming in C,C++, and Fortran on most platforms, instruction set architectures,and operating systems. It consists of a set of compiler directives, library routines, and environment variables that influence run-time behavior.
In the case of the C++ DLL, which is where the execution is actually happening, OpenMP involves using compiler directives to execute the filtering routines in parallel. For picture processing, each pixel of the input image has to be processed in order to apply the routine to that image. Parallelism offers an interesting way of optimizing the execution time by spreading out the work across multiple threads, which can work on different areas of the image.
#pragma omp parallel
In each filtering routine in the application, processing is implemented as a loop. The goal is to study every pixel in the image, one by one. The "#pragma omp parallel" compiler directive causes the loop exercise to be divided and distributed to the cores.
#pragma omp parallel for if(openMP)
for (int i = 0; i < height; ++i) {
auto offset = i * stride;
BGRA* p = reinterpret_cast<BGRA*>(inBGR + offset);
BGRA* q = reinterpret_cast<BGRA*>(outBGR + offset);
for (int j = 0; j < width; ++j) {
if (i == 0 || j == 0 || i == height - 1 || j == width - 1)
q[j] = p[j]; // if conv not possible (near the edges)
else {
BYTE R, G, B;
double red(0), blue(0), green(0);
// Apply the conv kernel to every applicable
// pixel of the image
for (int jj = 0, dY = -radius; jj < size; jj++, dY++) {
for (int ii = 0, dX = -radius; ii < size; ii++, dX++) {
int index = j + dX + dY * width;
// Multiply each element in the local
// neighborhood
// of the center pixel by the corresponding
// element in the convolution kernel
// For the three colors
blue += p[index].B * matrix[ii][jj];
red += p[index].R * matrix[ii][jj];
green += p[index].G * matrix[ii][jj];
}
}
// Writing the results to the output image
B = blue;
R = red;
G = green;
q[j] = BGRA{ B,G,R,255 };
}
}
}
Sample code for setting up parallel processing for BoxBlur.cpp
If you follow the comments in the code, "BoxBlur.cpp" is setting up offsets, handling calculations when edge conditions make convolution impossible, and applying the convolution kernel to each element for red, blue, and green colors.
#pragma omp parallel for if(openMP)
for (int i = 0; i < height; ++i) {
auto offset = i * stride;
BGRA* p = reinterpret_cast<BGRA*>(tmpBGR + offset);
BGRA* q = reinterpret_cast<BGRA*>(outBGR + offset);
for (int j = 0; j < width; ++j) {
if (i == 0 || j == 0 || i == height - 1 || j == width - 1)
q[j] = p[j]; // if conv not possible (near the edges)
else {
double _T[2];
_T[0] = 0; _T[1] = 0;
// Applying the two Sobel operators (dX dY) to
// every available pixel
for (int jj = 0, dY = -radius; jj < size; jj++, dY++) {
for (int ii = 0, dX = -radius; ii < size; ii++, dX++) {
int index = j + dX + dY * width;
// Multiplicating each pixel in the
// neighborhood by the two Sobel
// Operators
// It calculates the vertical and
// horizontal derivatives of the image
// at a point.
_T[1] += p[index].G * M[1][ii][jj];
_T[0] += p[index].G * M[0][ii][jj];
}
}
// Then is calculated the magnitude of the
// derivatives
BYTE a = sqrt((_T[0] * _T[0]) + (_T[1] * _T[1]));
// Condition for edge detection
q[j] = a > 0.20 * 255 ? BGRA{ a,a,a,255 } : BGRA{ 0,0,0,255 };
}
}
}
// Delete the allocated memory for the temporary grayscale image
delete tmpBGR;
}
return 0;
}
Parallelism structure for SobelEdgeDetector.cpp
In the second example of "omp parallel for" taken from "SobelEdgeDetector.cpp", similar filtering operations take place, with the edge detector working with grayscale pictures.
Memory Management
In software development, developers must be careful about memory management to avoid serious impacts on application performance. In the case of the Harris corner detector and the Shi-Tomasi corner detector, memory management is crucial to creating three matrices and storing the results of Sx, Sy and Sxy.
// Creating a temporary memory to keep the Grayscale picture
BYTE* tmpBGR = new BYTE[stride*height * 4];
if (tmpBGR) {
// Creating the 3 matrices to store the Sobel results, for each thread
int max_threads = omp_get_max_threads();
double *** Ix = new double**[max_threads];
double *** Iy = new double**[max_threads];
double *** Ixy = new double**[max_threads];
for (int i = 0; i < max_threads; i++) {
Ix[i] = new double*[size_kernel];
Iy[i] = new double*[size_kernel];
Ixy[i] = new double*[size_kernel];
for (int j = 0;j < size_kernel;j++) {
Ix[i][j] = new double[size_kernel];
Iy[i][j] = new double[size_kernel];
Ixy[i][j] = new double[size_kernel];
}
}
Setting up temporary memory for the Shi-Tomasi corner detector filter
Allocating such matrices for every pixel of the source would require considerable memory, and multithreading probably wouldn't be beneficial when applied. In fact, it could even result in slower calculations, due to the overhead of working with a large memory space.
In order to avoid memory issues and set up a scenario where multithreading makes the calculations faster, these three matrices can be considered as a set of matrices, with each available thread containing its own set of matrices. The application can then be set up to allocate, outside of the parallel section, as many sets of matrices as there are available threads for this application. To get the maximum number of threads the following function is used: "omp_get_max_threads()" from the "omp.h" file. This file is found with the rest of the header files in the ImageProcessing > External Dependencies directory.
As described at the Oracle* support site, this function should not be confused with the similarly named "omp_get_num_threads()".The "max" call returns the maximum number of threads that can be put to use in a parallel region. The "num" call returns the number of threads that are currently active and performing work. Obviously, those are different numbers. In a serial region "omp_get_num_threads" returns 1; in a parallel region it returns the number of threads that are being used.
The call "omp_set_num_threads" sets the maximum number of threads that can be used (equivalent to setting the OMP_NUM_THREADS environment variable).
In the processing loop, each thread accesses its proper set of matrices. These sets are stored in a dynamically allocated array of sets. To access the correct set the index of the actual thread is used with the function "omp_get_thread_num()".Once the routine is executed the three matrices are reset to their initial values, so that the next time the same thread has to execute the routine for another pixel, the matrix is already prepared for use.
Principle of Convolution
Image filtering is a good showcase for multi-core processing because it involves the principle of convolution. Convolution is a mathematical operation that accumulates effects; think of it as starting with two functions, such as f and g, to produce a third function that represents the amount of overlap as one function is shifted over another.
In this version of iteration, convolution is the process of adding each element of the image to its local neighbors, weighted by a kernel. By adding each element of the image to its local neighbors, weighted by the kernel, convolution can be used for blurring, sharpening, embossing, edge detection, and more. There are numerous resources available with a quick search, such as detailed discussions of kernels and image processing.
In the case of image filtering, convolution works with a kernel, which is a matrix of numbers. This kernel is then applied to every pixel of the image, with the center element of the convolution kernel placed over the source pixel (Px). The source pixel is then replaced by the weighted sum of itself and nearby pixels. Multithreading helps filter the image faster by breaking the process into pieces.
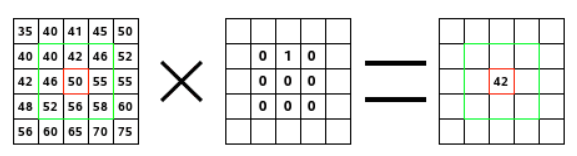
Figure 3. Convolution using weighting in a 3 x 3 kernel (source: GNU Image Manipulation Program).
In this example, the convolution kernel is a 3 x 3 matrix represented by the green box. The source pixel is 50, shown in red at the center of the 3 x 3 matrix. All local neighbors, or nearby pixels, are the pixels directly within the green square. The larger the kernel, the larger the number of neighbors.
In this case, the only weight different than zero is the second element of the first row and represented by a 1. All other elements in the 3 x 3 matrix are 0. The operation multiplies each element by zero, removing it, except for the single pixel represented by 42. So, the new source pixel is 42 x 1 = 42. Thus, the pixel just above the source pixel is overlapped by the weight 1 of the convolution kernel.
If you imagine each weighting as a fraction rather than zero, you can picture how images could be blurred by analyzing and processing each surrounding pixel.
Filtering Techniques
To see the result of a filtering technique, you'll have to build the project as described in the "Getting Started" section. Then double-click on the Image Filters > ImageFiltersWPF > Bin > Debug > ImageFiltersWPF.exe file.
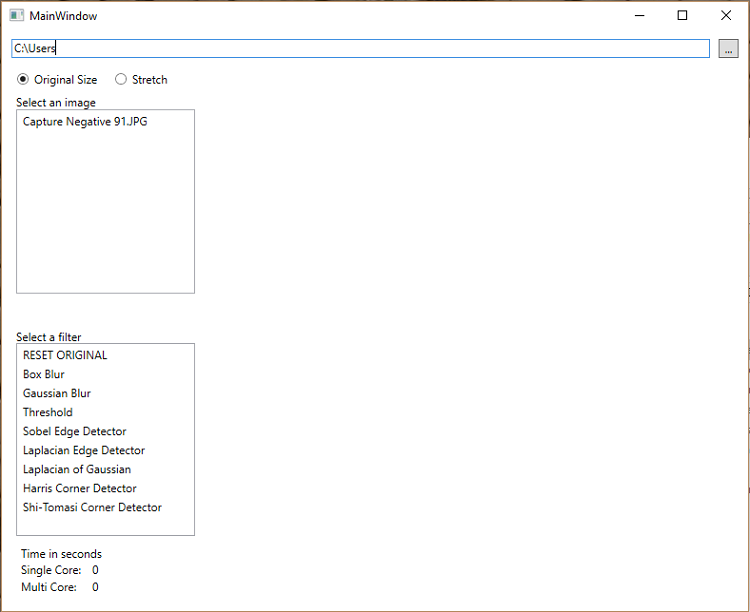
Figure 4. ImageFiltersWPF executable main window. Use the small gray box at the top-right corner of the screen to locate directories with images you want to experiment with.
The interface is very simple. You can select images on your system using the directory search feature in the gray box in the upper-right corner. Use the "Stretch" button to make sure an image completely fills the graphical user interface (GUI). Select an image, then apply a filter. Watch the "Time in seconds" calculations at the bottom-left of the interface to see how long a filter would take to apply in a multi-core system versus a system with a single core.
There are eight filters in all; each alters the original image, but some filters create more dramatic changes.
Box blur filter
A box blur is a spatial domain linear filter in which each pixel in the resulting image has a value equal to the average value of its neighboring pixels in the input image. Due to its property of using equal weights, it can be implemented using a simple accumulation algorithm, and is generally a fast way to achieve a blur. The name refers to the boxy, pixelated result.
The weights of the convolution kernel for the box blur are all the same. Assuming that we have a 3 x 3 matrix, this means that we have nine elements inserted into the matrix in total.
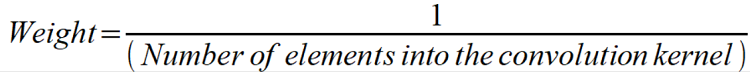
The weight for every element is calculated so that the sum of every element is 1.

Figure 5. The original image on the left is vivid, with good detail, while the image on the right has had the Box Blur effect applied.
When using the app, it was calculated that a single core system would take 0.1375 seconds to apply the Box Blur while a multi-core system, in this case with an Intel® Core™ i7-4220 processor, took 0.004 seconds.
Let's look in depth at what is going on in BoxBlur.cpp to understand the multithreading principles.
include "stdafx.h"
#include <fstream>
#include "omp.h"
using namespace std;
extern "C" __declspec(dllexport) int __stdcall BoxBlur(BYTE* inBGR, BYTE* outBGR, int stride, int width, int height, KVP* arr, int nArr)
{
// Pack the following structure on one-byte boundaries:
// smallest possible alignment
// This allows us to use the minimal memory space for this type:
// exact fit - no padding
#pragma pack(push, 1)
struct BGRA {
BYTE B, G, R, A;
};
Beginning of the BoxBlur.cpp file
First, the file is set up to include the "stdafx.h" header, a standard system include. Finally, omp.h is the header file that brings in OpenMP instructions.
BoxBlur then uses the extern "C" function to declare calls and variables. The rest of the C++ file is devoted to multi-core functionality. First, using "#pragma pack(push, 1)",the file defines how to efficiently handle a BGRA (blue green red alpha) color component packing structure on one-byte boundaries using the smallest possible alignment.
Next, the file declares "#pragma pack (pop)" to set up the default packing mode, defines the Boolean operator for whether multiple cores have been detected, sets up the convolution kernel, and allocates memory.
Finally, if there are multiple cores (OpenMP = true), the file uses "#pragma omp parallel for if (openMP)". The code determines offsets and casts, and handles situations at the edges where convolution is not possible. Results are written to the output image, and the allocated memory is cleared for the convolution kernel. There are similar sections of code in each of the filters.
Gaussian blur filter
Gaussian blur is the result of blurring an image by a Gaussian kernel to reduce image noise and reduce detail. It is similar to Box Blur filtering; each pixel in the image gets multiplied by placing the center pixel of the Gaussian kernel on the image pixel and multiplying the values in the original image with the pixels in the kernel that overlap. The values resulting from these multiplications are added up, and that result is used for the value at the destination pixel.
The weights of the elements of a Gaussian matrix N x N are calculated by the following:
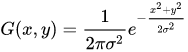
Here x and y are the coordinates of the element in the convolution kernel. The top-left corner element is at the coordinates (0, 0), and the bottom-right at the coordinates (N-1, N-1).
For the same reason as the Box Blur, the sum of every element has to be 1. Thus, at the end, we need each element of the kernel to be divided by the total sum of the weights of the kernel.
Threshold filter
The threshold routine is the only technique that does not use the convolution principle. Threshold filters examine each value of the input dataset and change all values that do not meet the boundary conditions. The result is that, if the luminance is smaller than the threshold, the pixel is turned to black; otherwise, it remains the same.

Figure 6. Threshold filtering example.
Sobel edge detection
The Sobel operator is an edge detector that relies on two convolutions by using two different kernels. These two kernels calculate the horizontal and vertical derivatives of the image at a point. Though its goal is different, it is used to detect the edges inside a picture. Applying such a kernel provides a score, indicating whether or not the pixel can be considered as being part of an edge. If this score is greater than a given threshold, it can be considered as part of an edge.
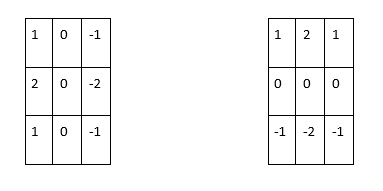
Figure 7. Sobel edge detection relies on two different kernels.
This means that for each pixel there are two results of convolution, Gx and Gy. Considering them as a scalar of a 2D vector, the magnitude G is calculated as follows:
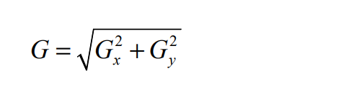
Laplacian edge detector
This filter technique is quite similar to Box Blur and Gaussian Blur. It relies on a single convolution, using a kernel such as the one below to detect edges within a picture. The results can be applied to a threshold so that the visual results are smoother and more accurate.
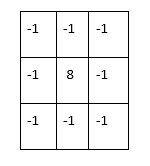
Laplacian of Gaussian
The Laplacian edge detector is particularly sensitive to noise so, to get better results, we can apply a Gaussian Blur to the whole image before applying the Laplacian filter. This technique is named "Laplacian of Gaussian".
Harris corner detector
Convolutions are also used for the Harris corner detector and the Shi-Tomasi corner detector, and the calculations are more complex than earlier filter techniques. The vertical and horizontal derivatives (detailed in the Sobel operator) are calculated for every local neighbor of the source pixel Px (including itself). The size of this area (window) has to be an odd number so that it has a center pixel, which is called the source pixel.
Thus, Sx and Sy are calculated for every pixel in the window. Sxy is calculated as Sxy = Sx * Sy.
These results are stored in three different matrices. These matrices respectively represent the values Sx, Sy, and Sxy for every pixel around the source pixel (and also itself).
A Gaussian matrix (the one used for the Gaussian blur) is then applied to these three matrices, which results in three weighted values of Sx, Sy, and Sxy. We will name them Ix, Iy, and Ixy.
These three values are stored in a 2 x 2 matrix A:

Then a score k is calculated, representing whether that source pixel can be considered as a part of a corner, or not.
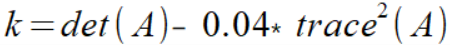
Then, if k is greater than a given threshold, the source pixel is turned into white, as part of a corner. If not, it is set to black.
Shi-Tomasi corner detector
This detector is based on the Harris corner detector; however, there is a change relating to the condition of corner detection. This detector has better performance than the previous one.
Once the matrix A is calculated, in the same way as above, the eigenvalues and of the matrix A are calculated. The eigenvalues of a matrix are the solutions of the following equation det (A) = 0.
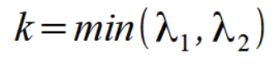
As with the Harris corner detector, with regard to the value of k, this source pixel will be or will not be considered as part of a corner.

Figure 8. Example of Shi-Tomasi corner detector filter, resulting in almost total conversion to black pixels. The filtering took 61 seconds using a single core, versus 14 seconds using multiple cores.
Conclusion
This C++ DLL application is a good example of how important it is to apply multithreading techniques to software development projects. In almost every scenario, the calculations involved on a four-core system to apply the various filters required about three times as long to complete using a single core versus using multi-core techniques.
Developers should not expect to get an N times speedup when running a program parallelized using OpenMP on an N processor platform. According to sources, there are several reasons why this is true:
- When a dependency exists, a process must wait until the data it depends on is computed.
- When multiple processes share a nonparallel proof resource (like a file to write in), their requests are executed sequentially. Therefore, each thread must wait until the other thread releases the resource.
- A large part of the program may not be parallelized by OpenMP, which means that the theoretical upper limit of speedup is limited, according toAmdahl's law.
- N processors in symmetric multiprocessing(SMP) may have N times the computation power, but thememory bandwidthusually does not scale up N times. Quite often, the original memory path is shared by multiple processors, and performance degradation may be observed when they compete for the shared memory bandwidth.
- Many other common problems affecting the final speedup in parallel computing also apply to OpenMP, likeload balancingand synchronization overhead.
With current systems powered by processors such as the Intel® Core™i9-7980XE Extreme Edition processor, which has 18 cores and 36 threads, the advantages of developing code that is optimized to handle multithreading is obvious. To learn more, download the app, analyze it with an integrated development environment such as Microsoft Visual Studio, and get started with your own project.
Appendix A. About ImageFiltersWPF
ImageFiltersWPF is a Windows* WPF client application that uses Extensible Application Markup Language (XAML) to display its GUI. The entry point into this app is MainWindow.xaml/MainWindow.xaml.cs. Along with the main window are several supporting classes to help keep functionality clean.
ImageFileList.cs
This class's primary function is to generate a list of image files that can be selected in order to apply filters.
ImageFilterList.cs
This is a very simple list that encapsulates a list of the filters that the C++ DLL provides. Once created, it is used by the GUI element lbImageFilters.
BitmapWrapper.cs
This class accepts a source bitmap image and takes that bitmap and turns it into a byte array that can be consumed by the C++ DLL.
ImageProcessWrapper.cs
This class loads up the DLL and supplies the function to call, which passes the byte arrays to the DLL.
MainWindow.xmal.cs
This is the MainWindow GUI code. This function gets the current filter name and sends the bitmapwrapper instance to the DLL. It does this twice, once for single core, then again as multi-core. After each of those run, it updates labels that contain the number of seconds it took to process the image. Once the processing is complete, the new image is displayed.