10/3/2024
Genetic algorithms (GA) are computational techniques inspired by the process of natural selection to solve constrained and unconstrained optimization problems. These algorithms are usually applied to various optimization problems, which are NP-hard, where finding a solution by standard methods consumes time and resources. GAs are based on an analogy of biological evolution and how human chromosomes behave.
This article demonstrates a code example on how to implement a general GA and perform an offload computation to a GPU using numba-dpex for Intel® Distribution for Python*.
Operations in GAs
For GAs, it is possible to obtain a high-quality result based on three important biology-inspired operations: selection, crossover, and mutation. To apply GAs to a specific problem, it is important to define the representation of the chromosome and the GA operations.
Selection
This is the process of selecting a mate and recombining it to create offspring. Parent selection is crucial for the convergence rate of GA as good parents drive individuals to better and fitter solutions.
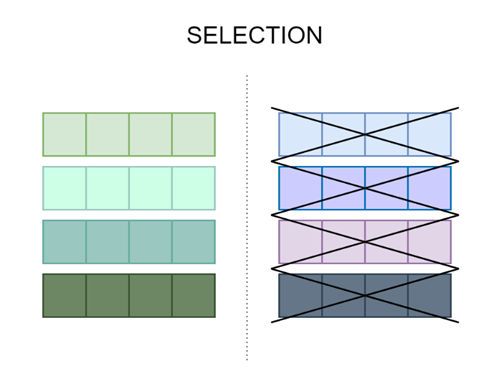
Figure 1. An example of the selection process where half of the chromosomes are removed from the next generation.
The selection process usually requires some additional algorithms that will determine which chromosomes will become parents.
Crossover
This process is the same as biological crossover. Here, more than one parent is selected, and one or more offspring are produced using the parents' genetic materials.
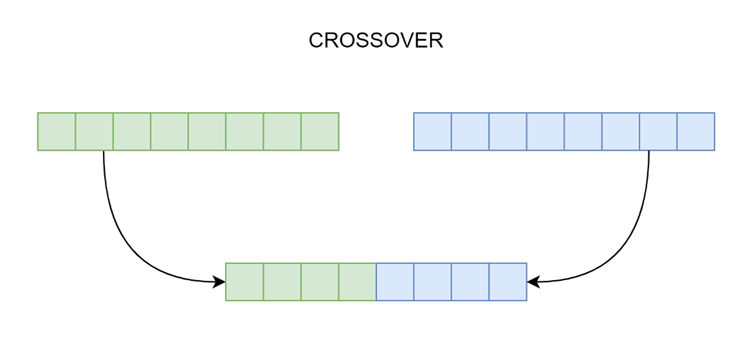
Figure 2. An example of a crossover operation.
The crossover operation creates child genomes from selected parent chromosomes, as shown in figure 2. It can be a one-point crossover and only one child genome is created. The first part of the child genome comes from the first parent and the second half from the second parent.
Mutation
A small, random tweak in the chromosome provides a new solution. It is used to maintain and introduce diversity in the genetic population and is usually applied with a low probability.

Figure 3. An example of a mutation operation where one chromosome value is changed.
The mutation operation can change the chromosome as shown in figure 3.
Optimize Genetic Algorithms with Intel® Distribution for Python*
Intel® Distribution for Python* helps developers achieve near-native code performance using libraries like Intel® oneAPI Math Kernel Library (oneMKL) and Intel® oneAPI Data Analytics Library (oneDAL) . Researchers and developers can scale compute-intensive Python code from laptops to powerful servers using optimized NumPy, SciPy, and Numba*.
To optimize the genetic algorithm with Intel Distribution of Python, use Data Parallel Extension for Numba* ( numba-dpex ) range kernel. This kernel represents the simplest form of parallelism and data-parallel running over a set of work items with each work item representing a logical thread of running.
Let's look at the example implementation of the kernel for a vector-add operation:
import dpnp
import numba_dpex
@numba_dpex.kernel
def vector_add(item: numba_dpex.kernel_api.Item, a, b, c):
i = item.get_id(0)
c[i] = a[i] + b[i]
To run this code, create all three vectors, a, b and c, where a and b are filled with the data, and c stores the result of the operation. Then, you need to send the vectors to a specific device, like a GPU, and then run the kernel as follows:
N = 1024
a = dpnp.ones(N, device="gpu")
b = dpnp.ones_like(a, device="gpu")
c = dpnp.zeros_like(a, device="gpu")
numba_dpex.call_kernel(vector_add, numba_dpex.kernel_api.Range(N), a, b, c)
In the previous code, the vector-add operation was run on a GPU and the result was stored in vector c. Similarly, for any other function or any other algorithm, the implementation looks the same.
Code Implementation
To create the general GA and optimize the algorithm to run on GPUs using the numba-dpex for Intel Distribution for Python, see the code example . It also explains how to implement different operations of GA such as selection, crossover, and mutation and how to adjust these methods to other optimization problems.
1. Set up the environment and import the libraries:
import numpy as np
import time
import random
import math
2. Initialize the population by setting the following:
- Population: 5,000
- Chromosome size: 10
- Generations: 5.
Each chromosome contains 10 random floats between 0 and 1. To reproduce the results later, set the seed as follows:
random.seed(1111)
pop_size = 5000
chrom_size = 10
num_generations = 5
fitnesses = np.zeros(pop_size, dtype=np.float32)
chromosomes = np.zeros(shape=(pop_size, chrom_size), dtype = np.float32)
for i in range(pop_size):
for j in range(chrom_size):
chromosomes[i][j] = random.uniform(0,1)
3. Implement the GA by creating an evaluation method. This function is the baseline and comparison for numba-dpex . Here, the fitness of an individual is computed by an arbitrary set of algebraic operations on the chromosome.
def eval_genomes_plain(chromosomes, fitnesses):
for i in range(len(chromosomes)):
num_loops = 3000
for j in range(num_loops):
fitnesses[i] += chromosomes[i][1]
for j in range(num_loops):
fitnesses[i] -= chromosomes[i][2]
for j in range(num_loops):
fitnesses[i] += chromosomes[i][3]
if (fitnesses[i] < 0):
fitnesses[i] = 0
4. Implement the crossover operation: The inputs have two different chromosomes as the first and second parent. The output of the function returns one new chromosome.
def crossover(first, second):
index = random.randint(0, len(first) - 1)
index2 = random.randint(0, len(second) - 1)
child_sequence = []
for y in range(math.floor(len(first) / 2)):
child_sequence.append( first[ (index + y) % len(first) ] )
for y in range(math.floor(len(second)/ 2)):
child_sequence.append( second[ (index2 + y) % len(second) ] )
return child_sequence
5. Implement the mutation operation: This code example has a one percent chance to change every float in the chromosome to a different random number.
def mutation(child_sequence, chance=0.01):
child_genome = np.zeros(len(child_sequence), dtype=np.float32)
# Mutation
for a in range(len(child_sequence)):
if random.uniform(0,1) < chance:
child_genome[a] = random.uniform(0,1)
else:
child_genome[a] = child_sequence[a]
return child_genome
6. Implement the selection operation, which is the base for creating a new generation. Within this function, a new population is created after crossover and mutation operations.
def next_generation(chromosomes, fitnesses):
fitness_pairs = []
fitnessTotal = 0.0
for i in range(len(chromosomes)):
fitness_pairs.append( [chromosomes[i], fitnesses[i]] )
fitnessTotal += fitnesses[i]
# Sort fitness in descending order
fitnesses = list(reversed(sorted(fitnesses)))
sorted_pairs = list(reversed(sorted(fitness_pairs, key=lambda x: x[1])))
new_chromosomes = np.zeros(shape=(pop_size, chrom_size), dtype = np.float32)
# Roulette wheel
rouletteWheel = []
fitnessProportions = []
for i in range(len(chromosomes)):
fitnessProportions.append( float( fitnesses[i]/fitnessTotal ) )
if(i == 0):
rouletteWheel.append(fitnessProportions[i])
else:
rouletteWheel.append(rouletteWheel[i - 1] + fitnessProportions[i])
# New population
for i in range(len(chromosomes)):
# Selection
spin1 = random.uniform(0, 1)
spin2 = random.uniform(0, 1)
j = 0
while( rouletteWheel[j] <= spin1 ):
j += 1
k = 0
while( rouletteWheel[k] <= spin2 ):
k += 1
parentFirst = sorted_pairs[j][0]
parentSecond = sorted_pairs[k][0]
# Crossover
child_sequence = crossover(parentFirst, parentSecond)
# Mutation
child_genome = mutation(child_sequence)
# Add new chromosome to next population
new_chromosomes[i] = child_genome
return new_chromosomes
7. Run the prepared functions, starting with a baseline on a CPU. As the first population is initialized, each generation contains the following steps:
-
- Evaluation of the current population using the eval_genomes_plain function
- Create the next generation using a next_generation function
- Wipe fitnesses values, since the new generation was already created
The computation time for those operations is measured and printed. The first chromosome is also printed to show that the computations were the same on both CPU and GPU.
print("CPU:")
start = time.time()
# Genetic Algorithm on CPU
for i in range(num_generations):
print("Gen " + str(i+1) + "/" + str(num_generations))
eval_genomes_plain(chromosomes, fitnesses)
chromosomes = next_generation(chromosomes, fitnesses)
fitnesses = np.zeros(pop_size, dtype=np.float32)
end = time.time()
time_cpu = end-start
print("time elapsed: " + str((time_cpu)))
print("First chromosome: " + str(chromosomes[0]))
8. Run on a GPU: Start with a new population initialization (the same as step 2), and then implement an evaluation function for the GPU. The only difference between GPU and CPU implementation is that on GPUs you use a flatten data structure for chromosomes. Also, instead of having to loop over all the chromosomes, use kernels from numba-dpex and a global index.
import numba_dpex
from numba_dpex import kernel_api
@numba_dpex.kernel
def eval_genomes_sycl_kernel(item: kernel_api.Item, chromosomes, fitnesses, chrom_length):
pos = item.get_id(0)
num_loops = 3000
for i in range(num_loops):
fitnesses[pos] += chromosomes[pos*chrom_length + 1]
for i in range(num_loops):
fitnesses[pos] -= chromosomes[pos*chrom_length + 2]
for i in range(num_loops):
fitnesses[pos] += chromosomes[pos*chrom_length + 3]
if (fitnesses[pos] < 0):
fitnesses[pos] = 0
9. Similar to the CPU, the time for evaluation, creation of a new generation, and a fitness wipe is measured while a GPU is running. Send all the chromosomes and the fitness container to the chosen device. Then you can run a kernel with a defined range.
import dpnp
print("SYCL:")
start = time.time()
# Genetic Algorithm on GPU
for i in range(num_generations):
print("Gen " + str(i+1) + "/" + str(num_generations))
chromosomes_flat = chromosomes.flatten()
chromosomes_flat_dpctl = dpnp.asarray(chromosomes_flat, device="gpu")
fitnesses_dpctl = dpnp.asarray(fitnesses, device="gpu")
exec_range = kernel_api.Range(pop_size)
numba_dpex.call_kernel(eval_genomes_sycl_kernel, exec_range, chromosomes_flat_dpctl, fitnesses_dpctl, chrom_size)
fitnesses = dpnp.asnumpy(fitnesses_dpctl)
chromosomes = next_generation(chromosomes, fitnesses)
fitnesses = np.zeros(pop_size, dtype=np.float32)
end = time.time()
time_sycl = end-start
print("time elapsed: " + str(time_sycl))
print("First chromosome: " + str(chromosomes[0]))
Apply the same steps on other optimization problems. Define the chromosome, selection, crossover, mutation, and evaluation operations. The rest of running the algorithm is the same.
Run the previous code example and compare the performance of this algorithm while performing sequential running on a CPU and parallel running on a GPU. The code output illustrates that the performance speed increases using a numba-dpex parallel implementation that runs on a GPU.
Next Steps
- Incorporate Intel Distribution for Python into your workflow and accelerate performance with optimizations for NumPy, SciPy, and Numba that scale from laptops up to powerful servers.
- Feel free to contribute to the Intel Distribution for Python project on GitHub* .