Monte Carlo European Option Pricing for Intel® Xeon® Processors

Download [10KB]

Introduction

This is an update of the article Monte Carlo European Option Pricing with RNG Interface for Intel® Xeon Phi™ Coprocessor, which covered the technical details of the Monte Carlo methods and the random number generation with Intel® Math Kernel Library (Intel® MKL). In this article, we discuss the performance of the workload updated for Intel® Xeon® Scalable processors.

Code Changes

This section describes the changes in the source code from the previous version.

The source has been modified to read the input from the user to make the source run across various Intel® Xeon® platforms.

Another change includes a different method for random number stream generation. The new source uses a SIMD-oriented Fast Mersenne Twister pseudorandom number generator for improved performance. The random numbers generated are single precision for both the single- and double-precision versions.  

Code Access

Monte Carlo European Option Pricing for Intel® Xeon® processors is maintained by Nimisha Raut and available under the Intel Sample Source Code License Agreement.

To access the code and test workloads, download the MonteCarlo.tar.gz file attached to this article

Build and Run Directions

Here are the steps for rebuilding the program:

1. Install Intel® Parallel Studio on your system.
2. Untar the MonteCarlo.tar.
3. Type make to build the binaries for single and double precision.
   • For single precision: MonteCarloInsideBlockingSP.x
   • For double precision: MonteCarloInsideBlockingDP.x

   Where x is abbreviation for the platform as below:

   • avx512 – for Intel Xeon Scalable processors supporting Intel® Advanced Vector Extensions 512 (Intel® AVX-512) instruction set extensions
   • avx2 – for systems supporting Intel^® Advanced Vector Extensions 2 instruction set extensions
   • knl - for Intel® Xeon Phi™ processor x200 product family
   • sse4_2 – for systems supporting Intel® Streaming SIMD Extensions 4.2 (Intel® SSE4.2) instruction set extensions
   • scalar - scalar version
4. Make sure the host machine is powered by Intel Xeon processors. 

   $ lscpu
   Architecture:	x86_64
   CPU op-mode(s):	32-bit, 64-bit
   Byte Order:	Little Endian
   CPU(s):	80
   On-line CPU(s) list:	0-79
   Thread(s) per core:	2
   Core(s) per socket:	20
   Core(s) per socket:	2
   NUMA node(s):	2
   Vendor ID:	GenuineIntel
   CPU family:	6
   Model:	85
   Model name:	Intel(R) Xeon(R) Gold 6148 CPU @ 2.40GHz
   Stepping	4
   CPU MHz:	1000.000
   BogoMIPS:	4792.94
   Virtualization:	VT-x
   L1d cache:	32K
   L1i cache:	32K
   L2 cache	1024K
   L3 cache:	28160K
   NUMA node0 CPU(s):	0-19,40-59
   NUMA node1 CPU(s):	20-39,60-79

5. Set the environment variables.

   export OMP_NUM_THREADS=maximum threads supported on the system

   export KMP_AFFINITY=compact,granularity=fine
    

6. Run the MonteCarlo SP and DP versions. Below is an example run with output.

   $ ./MonteCarloInsideBlockingDP.avx512 112 1344k 256k 8k
   Monte Carlo European Option Pricing Double Precision
   
   Build Time       = Oct 26 2017 14:03:13
   Path Length      = 262144
   Number of Options= 1376256
   Block Size       = 8192
   Worker Threads   = 112
   
   Starting options pricing...
   Parallel simulation completed in 10.342098 seconds.
   Validating the result...
   L1_Norm          = 4.816983E-04
   Average RESERVE  = 12.554841
   Max Error        = 8.945331E-02
   Test passed
   ==========================================
   Time Elapsed = 10.342098
   Opt/sec      = 133073.192723
   ==========================================

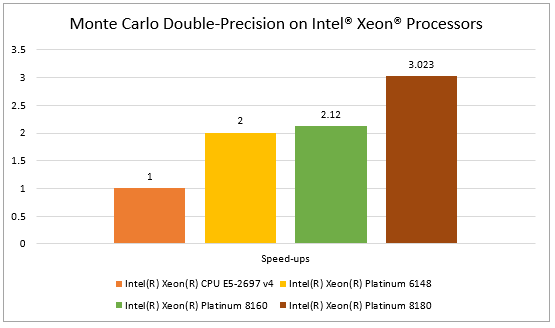
Performance across Generations of Intel® Xeon® processors

References

1. Case Study: Achieving High Performance on Monte Carlo European Option Using Stepwise Optimization Framework
2. Recipe: Monte Carlo European Option Pricing for Intel® Xeon Phi™ Processor
3. Monte Carlo European Option with Pre-generated Random Numbers for Intel® Xeon Phi™ Coprocessor

About the Author

Nimisha Raut is currently a software engineer with Intel’s Financial Services Engineering team in the Intel Software and Services Group. Her major interest is parallel programming and performance analysis on Intel processors and coprocessors and Nvidia GPGPUs. She received a Master’s degree in Computer Engineering from Clemson University and a Bachelor’s degree in Electronics Engineering from Mumbai University, India.