At Intel eXtreme Performance Users Group’s (IXPUG) Annual Conference 2025, hosted by the Texas Advanced Computing Center (TACC), researchers and software developers from industry, academia, science, and engineering came together to discuss how to best leverage Intel software development tools and high-performance computing platforms to accelerate compute, be productive, and get to answers faster.
In this article, we will summarize one of these reports highlighting how open-standard cross-architecture software development frameworks help advance fundamental science.
Multi-Scale Light-Matter Dynamics in Quantum Materials
Dr Nariman Piroozan of Intel Corporation, along with his co-authors Taufeq Mohammed Razakh, University of Southern California; Thomas Linker, Stanford University; Ye Luo, Argonne National Laboratory; Ken-ichi Nomura and Aiichiro Nakano, University of Southern California, used OpenMP and MPI together with the Intel® oneAPI DPC++/C++ Compiler to accelerate the study of light-matter interaction dynamics in quantum materials at the Aurora Exascale Supercomputer at Argonne Leadership Computing Facility, Argonne National Laboratory.
Consistent application of the principles of hierarchical parallelism allowed them to solve the multiscale Multiphysics heterogeneity challenge inherent in simulating multiple field and particle equations for light, electrons, and atoms over vast spatiotemporal scales. They divide the problem into not only spatial but also physical subproblems of small dynamic ranges and minimal mutual information, which are mapped onto the best available computational accelerator units, while metamodel algebra minimizes communication and precision requirements.
“Multi-Scale Light-Matter Dynamics in Quantum Materials on Aurora”
⇒ Replay the full presentation at IXPUG 2025.
⇒ Check out the full slide deck.
Presenter: Nariman Piroozan, Intel Corporation
Co-Authors: Taufeq Mohammed Razakh, University of Southern California; Thomas Linker, Stanford University; Ye Luo, Argonne National Laboratory; Ken-ichi Nomura and Aiichiro Nakano, University of Southern California.
The team of researchers presenting their progress and insights has been working closely together for some time on DC-Mesh, a divide-&-conquer Maxwell + Ehrenfest + surface-hopping algorithm, to simulate photo-induced quantum materials dynamics, which encapsulates the computational core of this effort.
High-Level Problem Architecture
DC-Mesh has been developed over several years as a method to study light-matter interaction. It implements a Modified Discrete Fourier Transform (MDFT), which is done in two parts:
- Solving simple partial differential equations with differential operators acting locally to describe local field dynamics (LFD). We are primarily talking about Maxwell equations and equations describing electron-light interaction. This is quite compute-intensive and implemented with the help of compute kernels offloaded onto GPUs
- Using screening mechanisms to approximately describe complex chemical reactions or quantum excitations. In other words, we simulate the reduction or moderation of quantum-level interactions between charged particles, taking advantage of the complex instruction set capabilities of CPUs.
Minimizing interactions between CPU and GPU computational components allows for the implementation of a globally sparse, locally dense solver using BLAS routines.
Divide and Conquer (DC) Approach of DC-Mesh
At [3min 30sec] Nariman details the divide and conquer approach a bit more.
The 3D space within which the light-matter interaction occurs is a union of overlapping domains. Kohn-Sham equations describe the electronic structure of matter or electron density in a potential energy field. Those are being solved for each domain.
Hamiltonian equations then describe the time evolution of the multi-domain system depending on the local electron density.
As a net result, all the local spatial domain densities and Kohn-Sham wave equations are summed up.
Inter-Domain scalability is achieved using MPI across nodes, and Intra-Domain scalability is achieved using OpenMP for GPU offload. (Figure 1)

Figure 1: Divide-&-Conquer Density Functional Theory
The first really compute-intensive operation is propagating the electron wave function. You start with a known wave function, pick a point from a set of points for an axis, update the wave function at grid points, and repeat this to cover all the mesh points in the system. This then represents the wave interaction with the matter grid layers.
Reordering, Blocking, Hierarchical Parallelism
Performance tuning comes from combining coarse-grain parallelism, blocking, and synchronization with hierarchical OpenMP parallelism for GPU offload.
[5min] into his talk, Nariman breaks down how this is implemented on a code block example.
1: void kin_prop (𝑝𝑠𝑖, 𝑎𝑙, 𝑏𝑙, 𝑏𝑢, 𝑝, 𝑑, 𝑁𝑜𝑟𝑏, 𝑁𝑟, 𝑁𝑥, 𝑁𝑦, 𝑁𝑧) {
2: complex<float> w;
// coarse grain parallelism
3: #pragma omp target teams distribute collapse(3)
4: for (int j=1; j <= Nr[1]; j++)
5: for (int k=1; k <= Nr[2]; k++) {
6: for (int ib=0; ib < (Norb+1)/block_size; ib++) {
7: complex<float> psi_old[block_size];
8: int begin = ib*block_size;
int end = min((ib+1)*block_size, norb);
// override synchronization
11: #pragma omp parallel for simd nowait
9: for (int n=begin; n < end; n++)
10: psi_old[n-begin] = psi[0][j][k][n];
8: for (int i=1; i <= Nr[0]; i++)
// override synchronization
9: #pragma omp parallel for simd nowait
// fine grain parallelism
10: for (int n=begin; n < end; n++) {
11: w = al*psi[i][j][k][n]
w += bl[i]*psi_old[n-begin]
12: …
13: # update psi_old ← psi [i][j][k][n]
14: # update psi [i][j][k][n] ← w
15: }
16: }
}
17: }
The first level of parallelism is achieved because the time evolution of a given point i requires just the knowledge of the wave function at the current time step and that of the previous time step within each plane.
The second level of parallelism can be achieved by calculating the wave function's propagation independently for each orbital, the size of which makes the biggest difference in the actual performance when the workload runs at scale. It is one of the key factors determining the size of the matrices used within the GEMM calls.

Figure 2: Wave Propagation Equations and GEMM.
Nariman then goes into additional detail on the optimization steps they employed, in addition to the use of the Intel® oneAPI Math Kernel Library (oneMKL) BLAS domain, leading to a 15.5% efficiency increase in numerically solving these equations when the approach is scaled to the use of up to 400 GPUs.
⇒ Check out [6min 30sec – 9min 5sec] for the detailed performance tuning discussion.
Extra Boost Through Mixed Precision
As part of oneMKL, there is the MKL_COMPUTE_MODE, which allows you to convert a float input matrix to various types with different precisions.
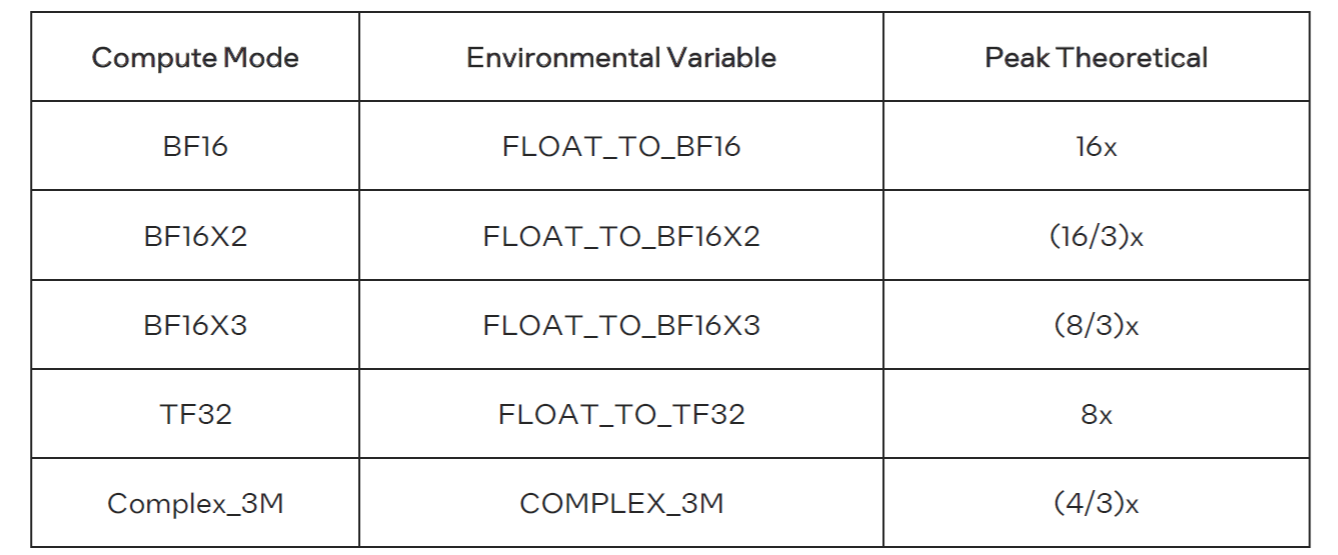
Figure 3: Supported Precision Conversions in oneMKL
Taking advantage of this and applying it to the CGEMM operations provides a significant additional performance boost. This approach of using lower precision or mixed precision for performance gains is very common in the AI/MLL world, but it can also be applied to HPC workloads.
The question arises whether a loss in precision is acceptable and still allows the computation to achieve its goals.
So, in FLOAT to BF16 conversion, for example, oneMKL internally converts single-precision float input data to sums of 1,2 or 3 BF16 values. It then uses the systolic arrays available on GPUs to multiply the resulting BF16 component matrices and accumulate them into a single-precision FP32. The resulting accuracy from BF16X3 will be close to that of the original FP32.
In the talk, the impact over simulation time on the slight reduction in accuracy is then discussed. For number of excited electrons, current density, and kinetic energy in atomic units the impact seems quite acceptable, given the performance boost.
⇒ The detailed discussion of the accuracy and performance tradeoff of mixed precision CGEMM starts [12min] into the presentation.
For 2048 orbitals using BF16 conversion, the measured performance improvement for GEMM amounts to a factor of 4x as reported in the setup used at the Aurora supercomputer platform. (configuration details on slide 17 of the presentation), and a significant improvement in time dissolution as well as scaling efficiency.
Accelerate and Scale Science with MPI, OpenMP, oneAPI, and oneMKL
Make your scientific workload scalable and highly performant with the latest in software development tools. Leverage and reuse concepts commonly used in AI for high-performance computing as well to find the right balance between precision and performance in your simulations. Find the answers to when querying nature faster.
You can download the Intel oneAPI DPC++/C++ Compiler as well as Intel® oneAPI Math Kernel Library and Intel® MPI Library on Intel’s oneAPI Developer Tools product page.
They are also available as part of the Intel® oneAPI HPC Toolkit and the Intel® oneAPI Base Toolkit, respectively, which include an advanced set of foundational tools, libraries, analysis, debug, and code migration tools.
Additional Resources: