New Instructions Supporting the Secure Hash Algorithm on Intel® Architecture Processors
July 2013
Executive Summary
This paper provides an introduction to the family of new instructions that support performance acceleration of the Secure Hash Algorithm (SHA) on Intel® Architecture processors. There are seven new SSE based instructions, four supporting SHA-1 and three for SHA-256. A detailed description of the Intel® SHA Extensions and example code sequences to fully process SHA-1 and SHA-256 blocks is provided.
Overview
The Secure Hash Algorithm (SHA) is a cryptographic hashing algorithm specified by the National Institute of Standards and Technology (NIST) in the Federal Information Processing Standards Publication 180 (FIPS PUB 180)[1]. The SHA family of algorithms is heavily employed in many of the most common cryptographic applications today. Primary usages of SHA include data integrity, message authentication, and digital signatures. One example of the impact of SHA is every secure web session initiation includes SHA-1, the latest protocols involve SHA-256 as well, and then the session data transfers between client and server are also commonly protected by one of the two algorithms. Given SHA-1 and SHA-256 make up the vast majority of secure hashing usage cases, the Intel® SHA Extensions were designed to support only those two algorithms (note SHA-224 is also implicitly supported with the SHA-256 instructions).
A hashing algorithm processes an arbitrary length message and results in a fixed length message digest. This is considered a one-way function, as the original message cannot be determined with absolute certainty based on the message digest. The Secure Hash Algorithm gets the name secure since it was designed to make it computationally infeasible to find any message that can be processed into a chosen message digest. Additionally, SHA is defined as secure because one cannot find two distinct messages that result in the same message digest. The security of the algorithms within the SHA family is outside the scope of this paper.
The Intel® SHA Extensions are a family of seven Streaming SIMD Extensions (SSE) based instructions that are used together to accelerate the performance of processing SHA-1 and SHA-256 on Intel® Architecture processors. Given the growing importance of SHA in our everyday computing devices, the new instructions are designed to provide a needed boost of performance to hashing a single buffer of data. The performance benefits will not only help improve responsiveness and lower power consumption for a given application, it may enable developers to adopt SHA in new applications to protect data while delivering to their user experience goals. The instructions are defined in a way that simplifies their mapping into the algorithm processing flow of most software libraries, thus enabling easier development.
Secure Hash Algorithm Introduction
The process of SHA to calculate the message digest has two phases. First is the preprocessing of the message to pad it out to a 64 byte multiple with the length of the message embedded in the last 8 bytes. The message is then split into 64 byte blocks to be processed in the next phase. The second phase is the hash computation, which has two main components itself. One is the message schedule which takes the 64 byte block and expands it into 32-bit dwords to be processed per round, and the other is the absorption of a given rounds message dword into the working variables. The Intel® SHA Extensions only focus on the compute-intensive hash computation; a padding discussion will not be included in this paper.
The message schedule calculation for SHA-1 is the following:
For i=0 to 79
If (0 ≤ i ≤ 15)
Wi = Mi
Else
Wi = ROL1(Wi-3 XOR Wi-8 XOR Wi-14 XOR Wi-16)
Where Wi is a 32-bit dword to be used in the ith round of the hash computation and Mi is the ith 32-bit dword in the 64 byte message to be hashed. ROL is a rotate left operation.
For SHA-256, the message schedule includes the σ functions, which use the ROR (rotate right) and SHR (shift right) operations:
For i=0 to 63
If (0 ≤ i ≤ 15)
Wi = Mi
Else
Wi = σ1(Wi-2) + Wi-7 + σ0(Wi-15) + Wi-16
Where σ0(W) is ROR7(W) XOR ROR18(W) XOR SHR3(W) and σ1(W) is ROR17(W) XOR ROR19(W) XOR SHR10(W).
The rounds function for SHA-1 is the following:
For i=0 to 79
T = ROL5(A) + fi(B, C, D) + E + Ki + Wi
E = D
D = C
C = ROL30(B)
B = A
A = T
Where A, B, C, D, and E are the five 32-bit working variables, K is one of four constant values (based on rounds 0-19, 20-39, 40-59, and 60-79), and f is one of four functions based on the same rounds intervals as K.
The rounds function for SHA-256 is the following:
For i=0 to 63
T1 = H + Σ1(E) + Ch(E,F,G) + Ki + Wi
T2 = Σ0(A) + Maj(A,B,C)
H = G
G = F
F = E
E = D + T1
D = C
C = B
B = A
A = T1 + T2
Where A, B, C, D, E, F, G, and H are the eight 32-bit working variables, K is one of 64 constant values, and Σ1(), Σ0(), Ch(), and Maj() are logical functions.
Intel® SHA Extension Definitions
The Intel® SHA Extensions are comprised of four SHA-1 and three SHA-256 instructions. There are two message schedule helper instructions each, a rounds instruction each, and an extra rounds related helper for SHA-1. All instructions are 128-bit SSE based, which use XMM registers. The SHA instructions are non-SIMD although they are defined with XMM width operands, whereas all the other supporting SSE instructions (e.g. ADD, XOR, AND) use dword sized lanes.

Table 1: Intel® SHA Extensions Definitions (rw – Read/Write, r – Read Only)
SHA-1
To aid with the message schedule component of SHA-1, there are two instructions called sha1msg1 and sha1msg2. The first instruction, sha1msg1, is intended to accelerate the Wt-14 XOR Wt-16 portion of the message schedule calculation. The second instruction, sha1msg2, is intended to accelerate Wt-3 XOR the previously calculated Wt-8 XOR Wt-14 XOR Wt-16 then do the rotate left by 1 of the result to finalize the message schedule for four consecutive 32-bit dwords (note Wt-8 is expected to be XOR’d with the result of sha1msg1 using the pxor instruction).
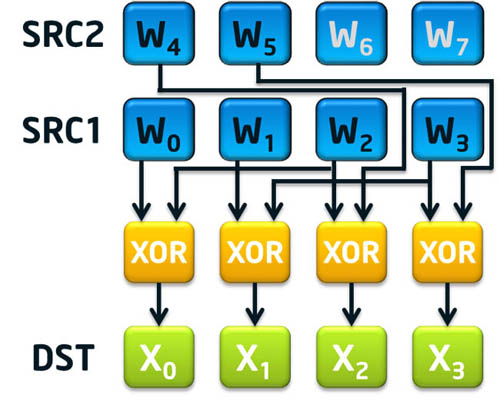
Figure 1: SHA1MSG1 xmm1, xmm2/m128 (The grayed out words are unused)

Figure 2: SHA1MSG2 xmm1, xmm2/m128
The SHA-1 specification for the hash computation of a block of message data is 80 rounds. The rounds instruction, sha1rnds4, performs four of these rounds at once. The instruction was designed to be four rounds because four of the five 32-bit SHA-1 working variables (A, B, C, and D) can be updated in one 128-bit destination XMM register. The inputs to sha1rnds4 are the working variables (A, B, C, and D), four 32-bit message dwords packed in a single XMM, with the E working variable added to W0, and an immediate value specifying which logic function (f()) and constant (K) to use for this rounds processing.
SHA1RNDS4 xmm1, xmm2/m128, imm8
| IF (imm8[1:0] == 0) THEN f() ← f0(), K ← K0; ELSE IF (imm8[1:0] == 1) THEN f()← f1(), K ← K1; ELSE IF (imm8[1:0] == 2) THEN f()← f2(), K ← K2; ELSE IF (imm8[1:0] == 3) THEN f()← f3(), K ← K3; |
A0 ← SRC1[127:96]; B0 ← SRC1[95:64]; C0 ← SRC1[63:32]; D0 ← SRC1[31:0]; |
W0E ← SRC2[127:96]; W1 ← SRC2[95:64]; W2 ← SRC2[63:32]; W3 ← SRC2[31:0]; |
Table 2: SHA1RNDS4 Inputs
Rounds operation:
Round i = 0 operation:
A1 ← f(B0, C0, D0) + (A0 ROL 5) + W0E + K;
B1 ← A0;
C1 ← B0 ROL 30;
D1 ← C0;
E1 ← D0;
FOR i = 1 to 3
Ai+1 ← f(Bi, Ci, Di) + (Ai ROL 5) + Wi + Ei + K;
Bi+1 ← Ai;
Ci+1 ← Bi ROL 30;
Di+1 ← Ci;
Ei+1 ← Di;
ENDFOR
Rounds output:
DEST[127:96] ← A4;
DEST[95:64] ← B4;
DEST[63:32] ← C4;
DEST[31:0] ← D4;
Notice in the above rounds definition that the working variables are assigned based on some form of the value of the adjacent variable a round earlier (B=A, C=B ROL 30, D=C, and E=D). Looking at this from the perspective of processing four rounds at once, the value of the fifth working variable, E, becomes simply A rotated left 30 bits. This property of the specification lends itself to an easy calculation of the variable E four rounds from the current round. The sha1nexte instruction exists to do the simple rotate and then add the result to one of the message dwords to be supplied to the sha1rnds4 instruction. The addition is necessary because with only two 128-bit XMM registers available to supply the sha1rnds4 instruction and 9 32-bit values required to do four rounds, one of the 32-bit values has to be absorbed somewhere. Fortunately the SHA-1 specification adds the E variable with the current round message dword as part of the function to set A. Therefore the sha1nexte instruction handles the addition for the first of the four rounds to be calculated in sha1rnds4.
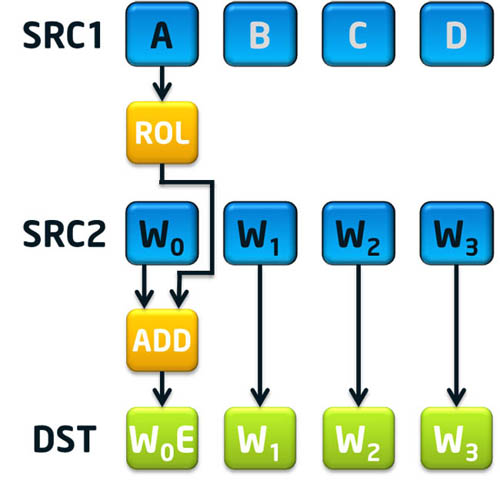
Figure 3: SHA1NEXTE xmm1, xmm2/m128
SHA-256
To aid with the message schedule component of SHA-256, there are two instructions called sha256msg1 and sha256msg2. The first instruction, sha256msg1, calculates the σ0(Wt-15) + Wt-16 portion of the message schedule calculation. The second instruction, sha256msg2, is intended to accelerate σ1(Wt-2) + the previously calculated Wt-7 + σ0(Wt-15) + Wt-16 to finalize the message schedule for four consecutive 32-bit dwords (note Wt-7 is expected to be added to the result of sha256msg1 using the paddd instruction).

Figure 4: SHA256MSG1 xmm1, xmm2/m128

Figure 5: SHA256MSG2 xmm1, xmm2/m128
The SHA-256 specification for the hash computation of a block of message data is 64 rounds. The rounds instruction, sha256rnds2, performs two of these rounds at once. The instruction was designed to be two rounds to simplify the assignment of the eight 32-bit working variables (A, B, C, D, E, F, G, and H). The variables C, D, G, and H are stored in one 128-bit XMM register and A, B, E, and F are stored in another XMM register. Once sha256rnds2 is executed, the XMM register originally containing CDGH is updated with the new ABEF values two round calculations later. The SHA-256 specification is such that the values of CDGH after two rounds are the original values of ABEF. This is a very simple property that the sha256rnds2 instruction makes use of, hence the non-obvious ordering of working variables. The third input to sha256rnds2 is the message dwords (Wn) added to the round constants (Kn). This W+K value must be in the architectural XMM0 register, since the register is implicitly used by the instruction.
SHA256RNDS2 xmm1, xmm2/m128, <XMM0>
| C0 ← SRC1[127:96]; D0 ← SRC1[95:64]; G0 ← SRC1[63:32]; H0 ← SRC1[31:0]; |
A0 ← SRC2[127:96]; B0 ← SRC2[95:64]; E0 ← SRC2[63:32]; F0 ← SRC2[31:0]; |
WK0 ← XMM0[31:0]; WK1 ← XMM0[63:32]; |
Table 3: SHA256RNDS2 Inputs
Rounds operation:
FOR i = 0 to 1
Ai+1 ← Ch(Ei,Fi,Gi) + Σ1(Ei) + WKi + Hi +Maj(Ai,Bi,Ci)+ Σ0(Ai);
Bi+1 ← Ai;
Ci+1 ← Bi;
Di+1 ← Ci;
Ei+1 ← Ch(Ei,Fi,Gi) + Σ1(Ei) + WKi + Hi + Di;
Fi+1 ← Ei;
Gi+1 ← Fi;
Hi+1 ← Gi;
ENDFOR
Rounds output:
DEST[127:96] ← A2; DEST[95:64] ← B2; DEST[63:32] ← E2; DEST[31:0] ← F2;
Using the Intel® SHA Extensions
The Intel® SHA Extensions can be implemented using direct assembly or through C/C++ intrinsics. The 16 byte aligned 128-bit memory location form of the second source operand for each instruction is defined to make the decoding of the instructions easier. The memory form is not really intended to be used in the implementation of SHA using the extensions since unnecessary overhead may be incurred. Availability of the Intel® SHA Extensions on a particular processor can be determined by checking the SHA CPUID bit in CPUID.(EAX=07H, ECX=0):EBX.SHA [bit 29]. The following C function, using inline assembly, performs the CPUID check:
int CheckForIntelShaExtensions() {
int a, b, c, d;
// Look for CPUID.7.0.EBX[29]
// EAX = 7, ECX = 0
a = 7;
c = 0;
asm volatile ("cpuid"
:"=a"(a), "=b"(b), "=c"(c), "=d"(d)
:"a"(a), "c"(c)
);
// Intel® SHA Extensions feature bit is EBX[29]
return ((b >> 29) & 1);
}
The following sections will demonstrate how to use the family of extensions to process a complete 64 byte block of data for SHA-1 and SHA-256.
SHA-1
SHA-1 requires 80 rounds of processing for every 64 byte block of data. Therefore, sha1rnds4 needs to be executed 20 times for every block. The most efficient way to implement SHA-1 is to do the message schedule calculations while performing the rounds processing. The ideal scenario is to be able to hide the entire message schedule processing under the latency of the rounds functionality. In other words, the rounds processing is the critical path and the latency of sha1rnds4 determines the performance of SHA-1 calculations.
The following will go through the main loop of processing a single 64 byte block of data for SHA-1:
First, save the working variables, A through E, for addition at the end of the loop. Note the working variables can be stored on the stack as opposed to xmm registers with little to no performance penalty. This is helpful in 32-bit applications.
movdqa ABCD_SAVE, ABCD movdqa E_SAVE, E0
Now the rounds processing can begin with rounds 0 through 3. Since the first 16 dwords of the message schedule are the actual message data to be hashed, the data needs to be read in from memory. Assume the value in GPR “DATA_PTR” is a pointer to the input data buffer in memory. Once read, the data typically needs to be byte shuffled to be in the proper byte order required by the Intel® SHA Extensions.
movdqu MSG0, [DATA_PTR + 0*16] pshufb MSG0, SHUF_MASK
The first four rounds do not require the sha1nexte instruction since the value in the E register should already be the actual E value. Therefore the message can be added directly to the register holding the E variable to be in the proper form expected by sha1rnds4. Before consuming the ABCD state variables, the value is stored in an alternate E variable register to be used in the next four rounds. Note the 0 input to sha1rnds4 indicating this use of the rounds instruction should process data as specified in the first 0-19 rounds. Every twenty rounds (every five instances of sha1rnds4 in the loop) the immediate value needs to be incremented.
paddd E0, MSG0 movdqa E1, ABCD sha1rnds4 ABCD, E0, 0
Now the next four rounds are ready to be processed. This time the sha1nexte instruction will be used with the E1 register saved prior to the first four rounds and the next four dwords of message data.
movdqu MSG1, [DATA_PTR + 1*16] pshufb MSG1, SHUF_MASK sha1nexte E1, MSG1 movdqa E0, ABCD sha1rnds4 ABCD, E1, 0
At this point MSG0 contains message dwords W0 through W3 and MSG1 contains W4 through W7. It is time to start using the SHA-1 message schedule related instructions to help with calculating W16 through W19. MSG0 will be consumed and will contain the result of the calculation to achieve Wt-14 XOR Wt-16.
sha1msg1 MSG0, MSG1
Rounds 8 through 11 can now be started, in a similar fashion to rounds 4 through 7. Note this time the E0 and E1 registers once again ping ponged back to the same usage as in rounds 0 through 3.
movdqu MSG2, [DATA_PTR + 2*16] pshufb MSG2, SHUF_MASK sha1nexte E0, MSG2 movdqa E1, ABCD sha1rnds4 ABCD, E0, 0
For the message scheduling, MSG1 and MSG2 are used in the same fashion as MSG0 and MSG1 in the previous four rounds. This pattern will continue by using sha1msg1 with the previous four rounds message data and the message data just consumed. The new addition to the message schedule calculation is an xor. The xor of MSG0 and MSG2 is to bring the Wt-8 data into the previous Wt-14 XOR Wt-16 calculation.
sha1msg1 MSG1, MSG2 pxor MSG0, MSG2
Rounds 12 through 15 are the last ones the message data needs to be read in from memory. During these rounds is where the final member of the SHA-1 family of instructions is used. The sha1msg2 instruction takes MSG0 and MSG3 to complete the calculation of W16 through W19 to be used in the next four rounds, 16 through 19.
movdqu MSG3, [DATA_PTR + 3*16] pshufb MSG3, SHUF_MASK sha1nexte E1, MSG3 movdqa E0, ABCD sha1msg2 MSG0, MSG3 sha1rnds4 ABCD, E1, 0 sha1msg1 MSG2, MSG3 pxor MSG1, MSG3
The pattern seen in rounds 12 through 15, excluding the memory read, continues up through rounds 64 to 67. Each time with the E variables ping ponging back and forth and the four different MSG variables cycling through.
sha1nexte E0, MSG0 movdqa E1, ABCD sha1msg2 MSG1, MSG0 sha1rnds4 ABCD, E0, 0 sha1msg1 MSG3, MSG0 pxor MSG2, MSG0
Since the message schedule is always ahead of the rounds calculation, the final rounds (68 through 79) will require fewer instructions. Note the use of the immediate 3 in the sha1rnds4 instruction usage to indicate being in the last 20 rounds of processing (60-79).
;; Rounds 68-71 sha1nexte E1, MSG1 movdqa E0, ABCD sha1msg2 MSG2, MSG1 sha1rnds4 ABCD, E1, 3 pxor MSG3, MSG1 ;; Rounds 72-75 sha1nexte E0, MSG2 movdqa E1, ABCD sha1msg2 MSG3, MSG2 sha1rnds4 ABCD, E0, 3 ;; Rounds 76-79 sha1nexte E1, MSG3 movdqa E0, ABCD sha1rnds4 ABCD, E1, 3
With the rounds processing complete, the final step is to add the saved working variables with the current state of the working variables. The ABCD addition is very straightforward. The addition of the current E variable is much more interesting. Since E0 contains the value of A from round 75, it needs to be rotated 30 prior to being added to the saved E value. Fortunately we can make use of the sha1nexte instruction to do the rotate and do the addition all at once.
sha1nexte E0, E_SAVE paddd ABCD, ABCD_SAVE
This completes the block processing and now the code can loop back to process another block or return with the final state.
SHA-256
The SHA-256 implementation is very similar to SHA-1. Some of the key differences are SHA-256 has only 64 rounds, the constants need to be added to the message data (it is not a part of the rounds instruction), and the message schedule requires more instructions for calculation.
The following will go through the main loop of processing a single 64 byte block of data for SHA-256:
The SHA-256 code starts the same way as SHA-1, by saving the working variables A through H for addition at the end of the loop. Note prior to the loop starting, the initial loading of the state variables is most likely not going to be from contiguous memory locations given the non-consecutive nature of the 32-bit variables in the 128-bit XMM registers. This is not a cause for concern since the shuffle in and back out occurs only outside the main processing loop, thereby becoming inconsequential in terms of performance.
movdqa ABEF_SAVE, STATE0 movdqa CDGH_SAVE, STATE1
Now the rounds processing can begin with rounds 0 through 3. The SHA-256 rounds instruction only processes two rounds at once; however, the code is optimally organized in a sequence to process four rounds at time. The same as with SHA-1, the initial 16 dwords of message data needs to be read in from memory and byte shuffled. One big change is the message data always needs to be stored in XMM0 for consumption by the rounds instruction. Therefore we need temporary message registers to save the dwords for later message schedule calculations. As mentioned, the constants defined in the SHA-256 specification need to be added to the message prior to the rounds instruction execution. Note the shuffle of MSG in between sha256rnds2 uses. This is because only two message dwords are consumed per rounds instance and there are four consecutive dwords in the 128-bit XMM0 register. One last observation to make is the usage of STATE0 and STATE1 with the sha256rnds2 instances. The two registers will ping pong back and forth throughout the entire block processing loop. The CDGH state input is a src/dest variable that becomes the new ABEF after the two rounds of processing. The ABEF input is simply the CDGH state input for the next sha256rnds2 execution due to the properties of the SHA-256 specification.
movdqu MSG, [DATA_PTR + 0*16] pshufb MSG, SHUF_MASK movdqa MSGTMP0, MSG paddd MSG, [SHA256CONSTANTS + 0*16] sha256rnds2 STATE1, STATE0 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1
The next four rounds follow the same pattern as the SHA-1 implementation. The rounds code is similar to the first four rounds with the addition of the first message schedule instruction instances. MSGTMP0 will be consumed and will contain the result of the calculation to achieve σ0(Wt-15) + Wt-16.
movdqu MSG, [DATA_PTR + 1*16] pshufb MSG, SHUF_MASK movdqa MSGTMP1, MSG paddd MSG, [SHA256CONSTANTS + 1*16] sha256rnds2 STATE1, STATE0 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1 sha256msg1 MSGTMP0, MSGTMP1
Rounds 8 through 11 look the same as the previous four rounds with the exception of the register usage for the new message dwords. The rest of the message schedule code takes shape with rounds 12 through 15. Since the Wt-7 term is not nicely aligned, there has to be some shifting code to add the value into the previous calculated σ0(Wt-15) + Wt-16 values. Once that term is added in, the value is an input to the sha256msg2 instruction which finishes the W16 through W19 calculation by adding in the σ1(Wt-2) term.
movdqu MSG, [DATA_PTR + 3*16] pshufb MSG, SHUF_MASK movdqa MSGTMP3, MSG paddd MSG, [SHA256CONSTANTS + 3*16] sha256rnds2 STATE1, STATE0 movdqa MSGTMP4, MSGTMP3 palignr MSGTMP4, MSGTMP2, 4 paddd MSGTMP0, MSGTMP4 sha256msg2 MSGTMP0, MSGTMP3 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1 sha256msg1 MSGTMP2, MSGTMP3
As seen in the SHA-1 implementation, starting at round 16 the code takes on a repeating pattern through rounds 48 through 51.
movdqa MSG, MSGTMP0 paddd MSG, [SHA256CONSTANTS + 4*16] sha256rnds2 STATE1, STATE0 movdqa MSGTMP4, MSGTMP0 palignr MSGTMP4, MSGTMP3, 4 paddd MSGTMP1, MSGTMP4 sha256msg2 MSGTMP1, MSGTMP0 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1 sha256msg1 MSGTMP3, MSGTMP0
The code for the last 12 rounds (52 through 63) is the following:
;; Rounds 52-55 movdqa MSG, MSGTMP1 paddd MSG, [SHA256CONSTANTS + 13*16] sha256rnds2 STATE1, STATE0 movdqa MSGTMP4, MSGTMP1 palignr MSGTMP4, MSGTMP0, 4 paddd MSGTMP2, MSGTMP4 sha256msg2 MSGTMP2, MSGTMP1 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1 ;; Rounds 56-59 movdqa MSG, MSGTMP2 paddd MSG, [SHA256CONSTANTS + 14*16] sha256rnds2 STATE1, STATE0 movdqa MSGTMP4, MSGTMP2 palignr MSGTMP4, MSGTMP1, 4 paddd MSGTMP3, MSGTMP4 sha256msg2 MSGTMP3, MSGTMP2 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1 ;; Rounds 60-63 movdqa MSG, MSGTMP3 paddd MSG, [SHA256CONSTANTS + 15*16] sha256rnds2 STATE1, STATE0 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1
Finally the state variables are added with the previously saved values and the loop can either process a new block or return.
paddd STATE0, ABEF_SAVE paddd STATE1, CDGH_SAVE
Using C/C++ Compiler Intrinsics
| __m128i _mm_sha1msg1_epu32(__m128i, __m128i); |
| __m128i _mm_sha1msg2_epu32(__m128i, __m128i); |
| __m128i _mm_sha1rnds4_epu32(__m128i, __m128i, const int); |
| __m128i _mm_sha1nexte_epu32(__m128i, __m128i); |
Table 4: SHA1 Instruction C/C++ Compiler Intrinsic Equivalent
| __m128i _mm_sha256msg1_epu32(__m128i, __m128i);
|
| __m128i _mm_sha256msg2_epu32(__m128i, __m128i);
|
| __m128i _mm_sha256rnds2_epu32(__m128i, __m128i, __m128i);
|
Table 5: SHA256 Instruction C/C++ Compiler Intrinsic Equivalent
The following provides a comparison of the usage of assembly versus intrinsics for the first four rounds of SHA-256:
Assembly:
;; Rounds 0-3 movdqu MSG, [DATA_PTR + 0*16] pshufb MSG, SHUF_MASK movdqa MSGTMP0, MSG paddd MSG, [SHA256CONSTANTS + 0*16] sha256rnds2 STATE1, STATE0 pshufd MSG, MSG, 0x0E sha256rnds2 STATE0, STATE1
Intrinsics:
// Rounds 0-3
msg = _mm_loadu_si128((__m128i*) data);
msgtmp0 = _mm_shuffle_epi8(msg, shuf_mask);
msg = _mm_add_epi32(msgtmp0,
_mm_set_epi64x(0xE9B5DBA5B5C0FBCFull,
0x71374491428A2F98ull));
state1 = _mm_sha256rnds2_epu32(state1, state0, msg);
msg = _mm_shuffle_epi32(msg, 0x0E);
state0 = _mm_sha256rnds2_epu32(state0, state1, msg);
Conclusion
SHA-1 and SHA-256 are two of the most common cryptographic algorithms in use today. The Intel® SHA Extensions are designed to accelerate SHA-1 and SHA-256 processing. Making use of the Intel® SHA Extensions on processors where available, is designed to provide a performance increase over current single buffer software implementations using general purpose instructions. This paper detailed the Intel® SHA Extensions and how to efficiently use the instructions when implementing SHA-1 and SHA-256.
Acknowledgements
We thank David Cote and Ray Askew for their substantial contributions to this work.
References
[1] FIPS Pub 180-2 Secure Hash Standard http://csrc.nist.gov/publications/fips/fips180-2/fips180-2.pdf
Authors
Sean Gulley, Vinodh Gopal, Kirk Yap, Wajdi Feghali, Jim Guilford, and Gil Wolrich are IA Architects with the DCSG Group at Intel Corporation.
Acronyms
IA Intel® Architecture
SHA Secure Hash Algorithm
SSE Streaming SIMD Extensions