Random Number Generation and Parallel Compute
GPUs have become increasingly powerful and are widely used for various computational tasks, including random number generation. Random numbers are essential in many applications, such as cryptography, simulation, and scientific computing. They play a key role in providing the random seeds for many different prediction scenarios from predictive maintenance, quantitative finance risk assessment, or earthquake and tsunami emergency response planning. GPUs offer a significant advantage in generating random numbers due to their parallel processing capabilities. This allows for generating many random numbers simultaneously, improving efficiency and speed. In the digital age, where data privacy and accuracy are paramount, generating random numbers on GPU is vital in scaling and accelerating highly accurate calculations, simulations, and prediction engines. It makes highly secure cryptography in banking, health sciences, and corporate security possible without impacting the end-user experience.
The Intel® oneAPI Math Kernel Library (oneMKL) is a high-performance math library that provides optimized functions for mathematical computations. It is designed to accelerate complex mathematical operations, such as linear algebra, fast Fourier transforms, and random number generation. oneMKL is part of the Intel® oneAPI Base Toolkit, a comprehensive set of development tools and libraries for building optimized high-performance applications targeting accelerated compute platforms.
The MRG32k3a[1] random number generator is a widely used algorithm for generating pseudo-random numbers for these more advanced use cases. It is a combined multiple recursive random number generator with a long period. Thus, it can produce a large set of unique random numbers before repeating. It is known for its good statistical properties, making it suitable for many different applications.
What if we can improve its performance even more by splitting the algorithm into several smaller tasks that can be processed simultaneously? We aim to increase performance by increasing the algorithm's parallelism level.
In this article, we introduce the addition of a sub-sequence parallelization method for MRG32k3a random number generator to oneMKL. While there are already existing methods for generating random numbers in the library, this article highlights the benefits of incorporating a sub-sequence parallelization technique.
Parallelization Approaches
There are various ways to generate random numbers in parallel. However, we need to consider the statistical correctness of the resulting sequence and generator period. The statistical randomness and the length of the period before a number repeats cannot be compromised. The following section explores the primary strategies for implementing such parallelization.
The standard implementation of MRG32k3a random number parallelization involves dividing the generation process equally among threads using the skip ahead[2] method (Figure 1). For instance, if we generate 100 random numbers with 10 threads, the first thread will generate the first 10 elements, the second thread will generate the next 10 elements, and so on. While this approach ensures consistent output, it also requires a highly computationally complex skip-ahead operation for each thread.

Figure 1. Types of Parallelization Approaches
The research outlined in a paper by Pierre L'Ecuyer et al. on “Object-Oriented Random-Number Package with Many Long Streams and Substreams” [4] demonstrates that the sequence produced by the MRG32k3a generator can be segmented into sub-sequences with a 2^67 element displacement (Figure1), and these can be recombined without creating any correlation in the resulting sequence.
This is indeed possible for the MRG32k3a algorithm, as it has a large period of 2191 elements. Each sub-stream is responsible for generating random numbers, which are then stored in memory with an offset equal to the total number of sub-streams (Figure. 2). For example, if there are 10 sub-streams and we want to generate 100 random numbers, the first sub-stream will generate the 1st, 11th, ... and 91st elements, while the second sub-stream will generate the 2nd, 12th, ... and 92nd elements, and so on.
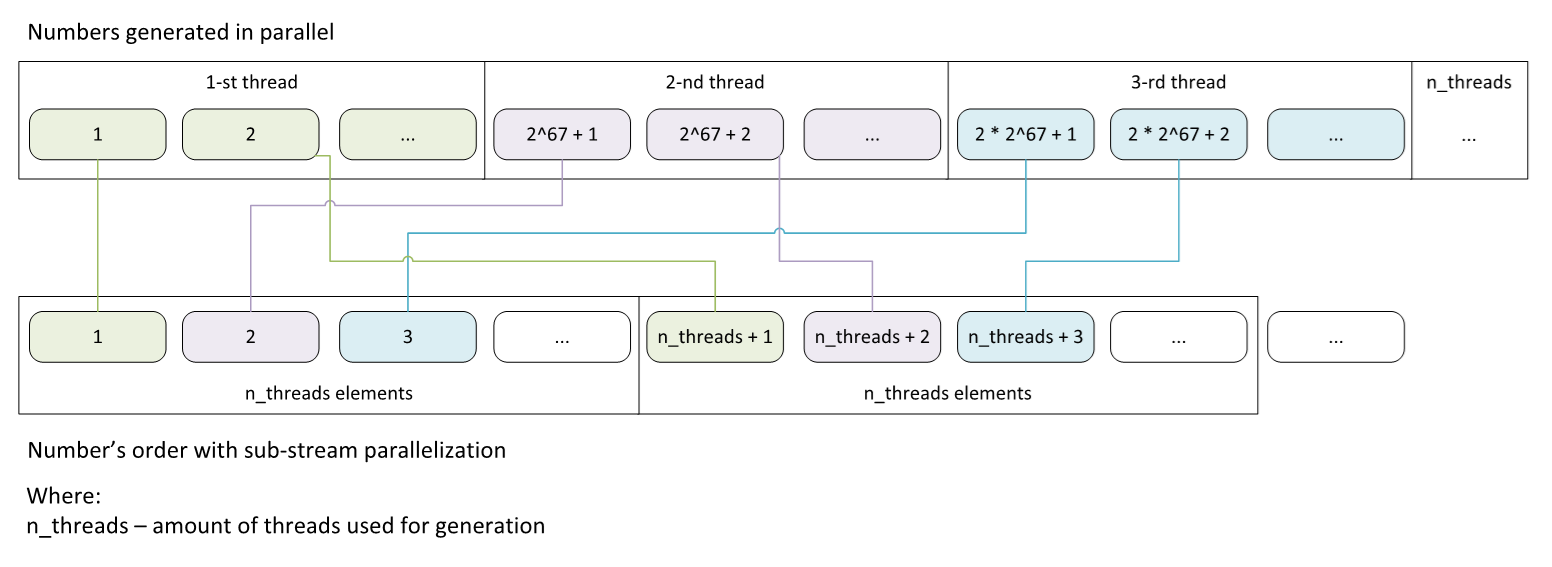
Figure 2. Approach for Generated Number Distribution into Memory.
Another popular method for generating random numbers in parallel involves assigning unique seeds to each thread. Although this approach allows to achieve performance scalability, there is no guarantee of statistical independency of the sequences with different seeds. When random numbers are generated using different seeds in parallel, there is a higher chance of generating similar or correlated sequences of numbers.
The sub-sequence parallelization method uses a single seed for generation, resulting in decent performance and guaranteeing a high-quality output sequence.
Usage of Sub-Sequences with oneMKL
You can use sub-sequence parallelization with oneMKL Host API by providing a method at the random number generator initialization stage (see Table 1).
|
|
| Generating n random numbers with standard parallelization approach. | Generating n random numbers with sub-sequence parallelization approach. |
Table 1. Updating the Generation Method for Uniformly Distributed Numbers with MRG32k3a.
To set the default number of sub-streams based on your hardware, pass optimal{}. Use custom{num_streams} option to manually select the optimal number of sub-streams for the specific task.
The order in which numbers are generated in a sequence with sub-stream parallelization is determined by the number of sub-streams, as shown above. By utilizing the "custom" option, the same result can be achieved when using different hardware and generator implementations.
It is also possible to generate numbers using the MRG32k3a generator and sub-sequence parallelization using the oneMKL Device API (Figure 3).
// ...
namespace rng_device = oneapi::mkl::rng::device;
// kernel with initialization of generators
queue.parallel_for({num_streams}, [=](std::size_t id) {
// initialize generators with an offset of 2^67 elements
rng_device::mrg32k3a<1> engine(seed, {0, 4096 * (id % num_streams)});
engine_ptr[id] = engine;
}).wait();
// generate random numbers
queue.parallel_for({num_streams}, [=](std::size_t id) {
auto engine = engine_ptr[id];
rng_device::uniform<Type> distr;
std::uint32_t count = 0;
while (id + (count * num_streams) < n) {
auto res = rng_device::generate(distr, engine);
result_ptr[id + (count * num_streams)] = res;
count++;
}
}).wait();
// ...
Figure 3. Example of sub-stream parallelization implementation using oneMKL Device API.
CuRAND and oneMKL RNG Interchangeability.
When transitioning an application from the current* (CUDA Random Number Generation) library to oneMKL, it is crucial to preserve the output sequence. Otherwise, the functionality might not be fully identical. This concern is addressed by using sub-sequence parallelization mode with oneMKL’s MRG32k3a random number generator.
In the cuRAND Host API, the MRG32k3a random number generator operates only in sub-sequence parallelization mode. In contrast, oneMKL’s standard implementation uses a sequential approach. As a result, these two implementations of the same random number generator will produce different sequences.
Switching to sub-sequence mode allows obtaining the same sequences if both random number generators have the same initialization seed.
The transition to oneMKL can be further simplified by using the Intel® DPC++ Compatibility Tool. It offers automated code transformation, analysis, and optimization capabilities. Furthermore, it allows for automatic transition from cuRAND to oneMKL’s RNG domain, preserving the output sequence.
Scalability while Preserving Randomness
Adding the sub-sequence parallelization method for the MRG32k3a random number generator in the Intel oneMKL library efficiently generates high-quality pseudo-random numbers on GPUs. Dividing the output sequence into multiple sub-streams that can be processed in parallel can achieve this without compromising statistical quality.
The sub-sequence technique finds the right balance between scalability and randomness for the MRG32k3a random number generator. The provided usage examples demonstrate how this method can be easily integrated into existing oneMKL workflows, allowing developers to take advantage of parallel computation on GPUs for random number generation. Incorporating this method into oneMKL improves usability and compatibility by facilitating the transition of applications from other GPU math libraries like cuRAND. This ultimately accelerates simulations, numerical analysis, and other applications relying on large volumes of high-quality random data, regardless of whether an application is best scaled to run on discrete Intel® Arc™ Graphics GPUs, integrated GPUs based on Intel® Xe2 Graphics, Intel® Data Center GPUs, or even third-party compute accelerators.
Get the Software
Download the Intel® oneAPI Math Kernel Library (oneMKL) stand-alone or as part of the Intel® oneAPI Base Toolkit, a core set of tools and libraries for developing high-performance, data-centric applications across diverse architectures.
Additional Resources
Here are more resources you may be interested in:
- Intel® oneAPI Math Kernel Library (oneMKL) - Data Parallel C++ Developer Reference
- Intel® oneAPI Math Kernel Library Link Line Advisor
- Intel® DPC++ Compatibility Tool
- oneMKL Random Number Generator Device Routines
- Random Number Generation with cuRAND* and oneMKL
References
[1] - Pierre L'Ecuyer, (1999) Good Parameters and Implementations for Combined Multiple Recursive Random Number Generators. Operations Research 47(1):159-164. https://pubsonline.informs.org/doi/10.1287/opre.47.1.159
[2] – oneMKL Data Parallel C++ Developer Reference Skip Ahead Method
[3] - Pierre L'Ecuyer, Richard Simard, E. Jack Chen, W. David Kelton, (2002) An Object-Oriented Random-Number Package with Many Long Streams and Substreams. Operations Research 50(6):1073-1075. https://doi.org/10.1287/opre.50.6.1073.358