Abstract
The generation of Huffman codes is used in many applications, among them the DEFLATE compression algorithm. The classical way to compute these codes uses a heap data structure. This approach is fairly efficient, but traditional software implementations contain lots of branches that are data-dependent and thus hard for general-purpose CPU hardware to predict. On modern processors with deep pipelines or super-scalar execution, the cost of these branch mispredicts can become the performance limiter.
We present here an alternate approach to the traditional heap, which takes advantage of the vector processing capabilities of modern processors. For a range of problem sizes that occurs often in widely used applications, this approach is faster than using a heap.
Huffman Code Generation Algorithm - Overview
Huffman codes (https://en.wikipedia.org/wiki/Huffman_coding) are variable length codes that represent a set of symbols with the goal of minimizing the total number of bits needed to represent a stream of symbols. They achieve this by assigning shorter length codes to symbols that occur more frequently, and longer codes to the rarer symbols.
The following talks in particular about generating Huffman codes in the context of DEFLATE (https://en.wikipedia.org/wiki/DEFLATE) compression. The basic ideas presented may be used in other contexts utilizing dynamic Huffman codes, although some of the details will vary.
The generation of Huffman codes, at least within the context of DEFLATE compression, consists in taking an array of histogram data (weights), where each entry is a count of the number of times that symbol or token appears in the output, and then computing a corresponding code length for that token that minimizes the dot-product of the weights and the token-lengths.
Typically, the sum of the weights is guaranteed to be less than 64k, so the weights can be stored as 16-bit integers. The time needed to compute the codes is a function of how many non-zero weights there are. In DEFLATE, there are up to 30 values for the distance codes (the D-tree), but there are up to 286 values for the Literal-Length codes (the LL-tree), so in general the time for the LL-tree generation is largest.
The basic Huffman algorithm can be summarized as:
- Insert the entries with non-zero weights into the heap array (https://en.wikipedia.org/wiki/Heap_(data_structure)).
- Add in extra elements (each with weight 1) until the heap has at least two elements.
- Convert the array into a heap.
- While there is more than one element in the heap:
- Remove two elements from the heap (the ones with the two smallest weights).
- Create a new element that is the parent of these elements.
- Add that new element to the heap.
- Compute the code length of each element as its depth in the tree.
- If the max code length is too big, adjust the tree so that its depth is within limits.
- Generate the code values from the lengths.
The most interesting steps here are steps 3 and 4. These are the steps that involve the heap. The good property of a heap is that the heap operations tend to take O(log n) time. The bad part is that each step tends to involve branches that may not be easily predicted.
This led us to the current work where we replaced these heap operations with Single Instruction Multiple Data (SIMD) operations. The idea was to do more overall operations, O(n), but to avoid the branch mispredict penalties.
Let’s look in more detail at these two steps.
Huffman Code Generation Algorithm - Details
First we will look at some details of the heap-based implementation (as implemented in a common library).
Heap-Based Algorithm
The tree array contains the element data. Each element contains two 16-bit values. Initially one of them contains the weight (frequency). The second one will point to the parent of this node. So after the heap steps, these elements will define the Huffman tree (with pointers pointing towards the root). Then during the code-generation process, these two values will be replaced with the generated code and the code length. The index into the tree array implicitly defines the token being represented.
The heap is an array of indices into the tree array.
In step 4, rather than removing two values and then inserting a new one, only one value is removed. Then the top value is replaced with the new value, and the heap is made back into a heap.
There is a separate array that holds the elements in increasing order of size. The index of the smallest and second smallest element (that is, the one removed and the one to be overwritten) are appended to this second array.
One detail is that associated with each node in the heap there is not only the frequency, but also a “depth,” where the depth of leaf node (one of the original nodes) is zero, and the depth of an added node is one greater than the max of the two child nodes’ depths. When comparing two nodes for size in the heap logic, one is looking for the node with the smallest frequency, or if two nodes have the same frequency, the one with the smaller depth.
At the end of this step, we have a list of nodes, ordered from smallest to largest, along with pointers from each child node to its parent. Note that the parent always has a larger frequency than its children, so if the list is traversed from largest to smallest, the parent node will always be processed before either of its children.
This is best illustrated with an example. Assume that we have eight initial nodes (0…7) with frequencies of 4, 1, 3, 7, 15, 2, 25, 9. Then after the above procedure we’ll have the following tree, where the solid circles are the original nodes (indices 0…7) and the dashed circles are the added nodes (indices 8…14). Each node is labeled with its index and its frequency.
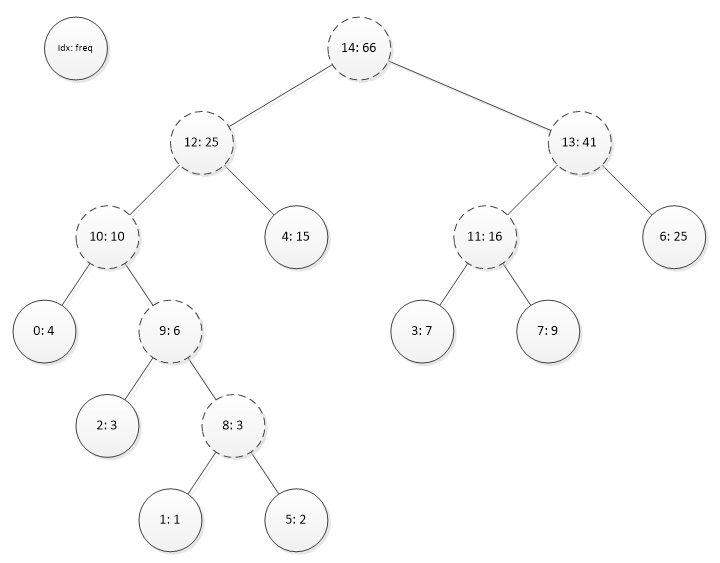
In the above figure, the parent pointers all point upward.
Associated with this is a list of nodes in increasing size: 1, 5, 2, 8, 0, 9, 3, 7, 10, 4, 11, 6, 12, 13, 14. In this list, all of the parent pointers point to the right.
Then the code just needs to set the bit-length of the right-most node (for example, node 14) to zero and traverse this list from right to left, setting the bit-length of each node to one greater than the length of its parent. In the above example, this would give the code lengths as {3, 5, 4, 3, 2, 5, 2, 3}.
Note that the code lengths can be derived from the code length counts and the ordered list of nodes (ignoring the non-leaf nodes). In the above example, the code length counts are {0, 2, 3, 1, 2}. The actual code lengths could be derived from walking the list and counting the various counts of codes, starting from the highest bit count. This is shown below:

From these code lengths, the actual codes can be derived as they are in DEFLATE decompression.
One wrinkle occurs when the tree is deeper than the maximum code length. For example, DEFLATE requires that no code be longer than 15 bits in length. If any of the nodes have a longer length, the tree must be adjusted. This can be done by finding a leaf node that is higher than maximum depth, moving it down, and putting one of the overflowing leaf nodes as its sibling. This also moves the sibling of the overflowing leaf node (which is also overflowing) one spot higher in the tree.
The actual tree does not need to be modified. It is sufficient to modify just the code length counts, and then to rebuild actual node code lengths as shown previously. In the above example, assume that the maximum code length was 4, so there are two overflowing bits. This can be corrected by making one of the 3-bit codes a 4-bit code, and making the two 5-bit codes also 4-bit codes (one as a sibling of the lowered 3-bit code, and one by moving up a level). This results in the code length counts {0, 2, 2, 4, 0}. This would result in code lengths {4, 4, 4, 3, 2, 4, 2, 3} as shown below:

One of the most time-consuming steps in this algorithm is the heap manipulation. This can involve poorly-predicted branches with their associated branch-mispredict penalties. In the following section, we look at an alternative using SIMD instructions.
SIMD Algorithm
The purpose of the (min) heap is to take a set of elements, find the smallest one, and to be able to remove that element from the set and repeat.
The basic idea here is to replace the heap with a simple array and to use SIMD instructions to find the smallest element. The trade-off is that we will in general perform more operations than if we had a heap, but the control flow will be regular and easily predicted.
Finding the Minimum of an Array
The code that we tested and profiled was written using the Intel® Advanced Vector Extensions 2 Intel® AVX2) instruction set. Its vector registers (YMM registers) are 256-bits wide, so they can operate on eight 32-bit dwords in parallel.
The basic operation is to find the minimum value in an array of dwords. We load a pair of YMM registers with the first 16 entries. Then we use the vpminud instruction to take the minimum within each lane between these registers and the next 16 entries.
At the end of the loop, we take the min between the two registers, and then use a series of shifts and min operations to get a final dword minimum value.
The performance-critical code looks like (this code loop processes two sets at the same time):
start_loop:
vpminud yfirst, yfirst, [addr_ptr + loop_idx]
vpminud ysecond, ysecond, [addr_ptr + 32 + loop_idx]
add loop_idx, 64
cmp loop_idx, total_size
jl start_loop
vpminud yfirst, yfirst, ysecond
final_block:
vperm2i128 ysecond, yfirst, ysecond, 0x01
vpminud yfirst, yfirst, ysecond
vpalignr xsecond, xfirst, xfirst, 8
vpminud xfirst, xfirst, xsecond
vpalignr xsecond, xfirst, xfirst, 4
vpminud xfirst, xfirst, xsecond
vmovd eax, xfirstData Structures
In the heap-based version, the heap contains indices of the tree nodes, and the tree nodes contain the frequencies and other information. However in the vector implementation, we need to have the necessary information in the array itself. Additionally, there are two sets of indices to be maintained.
One is the index of the element within the array. This is needed as the minimum operation returns the smallest value, but it doesn’t explicitly say where that value occurred. This index will be called the array-index.
The other is the index in the tree node array for the corresponding tree node. This will be called the tree-index.
Each dword in the array contains a bit-packed structure:
31:16 Frequency
15:9 Tree Depth
8:0 Array Index
This means that the minimum operation will return the entry with the lowest frequency, and for equal frequencies the lowest depth, and for equal frequencies and depth, the lowest index. More significantly, from the minimum value, one can determine the frequency and the index.
The elements just beyond the real data are initialized to all Fs, so that the minimum operation will not select them.
There is a parallel array that contains the corresponding tree indices.
When entries are moved around the main array, the corresponding entries in the tree-index table need to be moved in a similar manner.
Basic Loop
The basic loop looks like this:
- Find the minimum element of the array. Move the last element into the min element’s spot, and set the last element to all Fs.
- Find a second minimum element.
- Write the first and second tree pointers into the sorted order array.
- Create a new tree node that is the parent of the two removed nodes.
- Write that node’s information into the array in place of the second entry found above.
The rest of the processing is the same as in the heap version.
Performance
The performance results provided in this section were measured on an Intel® Core™ i7-4770 processor. The tests were run on a single core with Intel® Turbo Boost Technology off, and with Intel® Hyper-Threading Technology off and on.
Testing using data from standard corpora (for example, Calgary, Canterbury) indicated that when there were relatively few tree nodes, the heap approach was faster, but when there were relatively many tree nodes, the vector approach was faster.
We found a reasonable heuristic that if there were more than 140 elements, we should use the vector version, and when there were fewer, we should use the heap version. (This was after we had further optimized the heap version code.) We call that version the “hybrid” version. Note that this implies that the vector code will only ever be used when computing the Huffman codes for the LL tree.
We measured the performance of the heap version and the hybrid version on files from several standard corpora. For each block, we recorded how many non-zero LL codes there were and how many cycles the Huffman code generation took. We then plotted the cycles versus the number of codes. The results were:
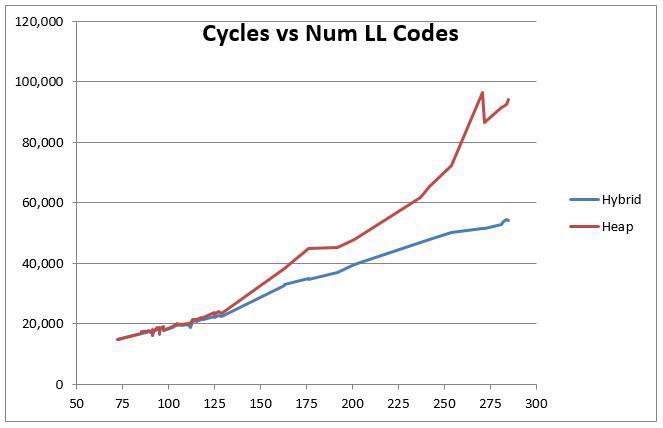
You can see that below 140 codes both versions perform identically, but above that point the heap-based code grows at a steeper angle than the hybrid version, so that by 285 LL codes, the difference is almost 2x.
The following table shows the net results and speedup for the corpus files. The cost is shown in terms of effective cycles per uncompressed byte for the old and new code under single-thread (ST) and two-thread (HT) scenarios. Note that decreasing the number of blocks created in a file is another way to achieve speedup with a tiny loss in ratio. Such techniques are possible (reducing the number of blocks, and therefore trees) and orthogonal to the technique described in this paper (reducing the cost per tree), but also help with the overall tree-construction overhead.
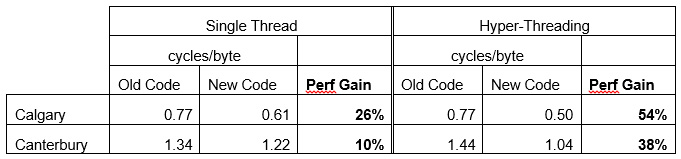
The data shown is just for the tree generation, and not for the overall compression (LZ77 matching, or encoding). The absolute cost and relative speedup is best under HT; this is largely due to the latencies involved in the code that are amortized with two threads.
Conclusion
We presented an efficient approach to generate Huffman codes, which takes advantage of the vector processing capabilities of modern processors. For sufficiently large problems, this approach is faster than that using a heap by ~2x. However, in the context of compression algorithms, such as Deflate, run on industry-standard corpus files, we see a net gain of up to 1.5x (due to the multiple types of trees being constructed of different sizes). The results were shown on processors with Intel AVX2; we expect additional gain with the wider SIMD units of processors supporting Intel® Advanced Vector Extensions 512.
Acknowledgements
We would like to acknowledge the work that Nancy Yadav did on this project. She was responsible for coding the new algorithm and optimizing the versions. She was also responsible for running the tests.
Authors
Jim Guilford and Vinodh Gopal are architects in the Intel Data Center Group, specializing in software and hardware features relating to cryptography and compression.