Tiling is an optimization technique, usually applied to loops, that orders the application data accesses to maximize the number of cache hits. The idea is simple to illustrate: Imagine you are combining two lists of numbers to enter into a grid, such as a multiplication table, but you are doing so with a multiply machine that repetitively multiplies two numbers and tediously enters results.
In real life, the tedious-to-enter numbers are probably huge data structures. In my current work, they are vectors containing thousands of complex numbers, and the multiply process involves complicated distance functions.
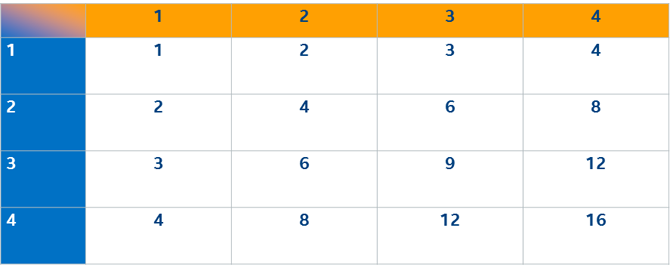
Using this multiply machine, you enter each left-hand side (LHS) number and each right-hand side (RHS) number 16 times. It makes no difference which order you do the cells, so the code usually does this simple order:
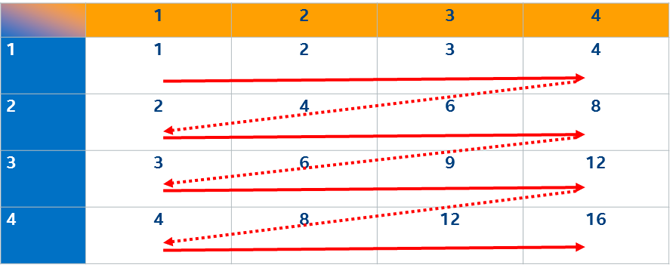
Let’s say a new version of the amazing multiply machine becomes available that lets you keep two numbers in the machine! If you do the cells in the same order as above, you need only enter each LHS number once, reusing it for the remaining 3 cells in the row. You must still enter the RHS number for each cell. Your total load count shrinks from 32 (16 LHS + 16 RHS) to 20 (4 LHS +16 RHS).
But there is a better order! After you load two of the RHS numbers into the machine, it is better to load a new LHS and reuse the loaded RHS than to continue along the row.
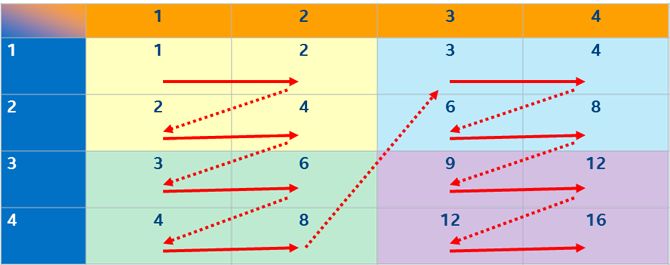
Now the order is (load#1 LHS1, load#2 RHS1), (reuse LHS1, load#3 RHS2), (load#4 LHS2, reuse RHS1), (reuse LHS2, reuse RHS2), (load#5 LHS3, reuse RHS1), (reuse LHS2, reuse RHS2), (load#6 LHS4, reuse RHS1), (reuse LHS4, reuse RHS22)… That means 6 loads to do the first two columns, and another 6 to do the second two columns, so you need 12 loads instead of 20.
This approach – breaking the big grid into tiles small enough that the tile LHS and RHS inputs all fit in the cache – is called tiling. There are other orders for doing the cells that will do slightly better than this, but in practice, this simple tiling gets almost all the possible win.
Importance of Tiling
While not obvious in the example above, tiling can reduce the required number of loads and stores to approximately the square root of the original number – a huge benefit on machines where each load from main memory is stalling the machine when it could be doing hundreds of instructions. Of course, if you have to write out each cell, that is also expensive and will probably dominate the resulting execution time. Still, tiling often means you can almost eliminate all the input costs and decrease execution time by 3x.
Unfortunately, tiling can be hard to tune because tile size choice depends on the data sizes, the algorithm, and the hardware. Investigate to determine if you can use a cache oblivious algorithm that does not require tuning to the data and the hardware.
Tile Loops
Below is a simple example of tiling a 2D algorithm. Note the code similarity of the two loops. If your code has just a few hot loops, the extra complexity is worth doing inline. However, if your code has many hot loops, you may want to encapsulate the outer loops into a reusable macro or template, placing the inner loop into either a virtual function or a lambda called from the shared outer scheduling code.
#include <algorithm>
#include <vector>
#include <iostream>
class Table {
std::vector<int> cells;
public:
const int side;
Table(int side) : side(side), cells(side*side) {}
int& operator()(int lhs, int rhs) { return cells[(lhs-1)*side+(rhs-1)]; }
} tableA(12), tableB(12);
void example() {
// Not tiled
for (int lhs = 1; lhs <= tableA.side; lhs++) {
for (int rhs = 1; rhs <= tableA.side; rhs++) {
tableA(lhs,rhs) = lhs*rhs;
}
}
// Tiled
// Note the deliberate inversion of the order going across the tiles with the order within the tile
// It results in better multi-level cache behavior
//
const int lhsStep = 2;
const int rhsStep = 2;
for (int rhsBegin = 1; rhsBegin <= tableB.side; rhsBegin+=rhsStep) {
int rhsEnd = std::min(tableB.side,rhsBegin+rhsStep);
for (int lhsBegin = 1; lhsBegin <= tableB.side; lhsBegin+=lhsStep) {
int lhsEnd = std::min(tableB.side,lhsBegin+lhsStep);
for (int rhs = rhsBegin; rhs <= rhsEnd; rhs++) {
for (int lhs = lhsBegin; lhs <= lhsEnd; lhs++) {
tableB(lhs,rhs) = lhs*rhs;
}
}
}
}
for (int lhs = 1; lhs <= tableA.side; lhs++) {
for (int rhs = 1; rhs <= tableA.side; rhs++) {
if (tableA(lhs,rhs) != tableB(lhs,rhs)) std::cerr << "Wrong value" << std::endl;
}
}
}Tile Algorithms
Tiling can be applied to more than just nested loops.
I first used tiling to great effect on a 1-MB machine in the mid-1980s. A compiler processed each function of the application code through a series of phases, and because neither all the compiler instructions nor all the application functions could fit in the 1-MB memory simultaneously, I modified the compiler to push as many functions as would fit through one phase, then bring in the next phase to push those functions through, and so on.
This general idea of separating scheduling from execution, and applying a reasonable amount of runtime effort to the scheduling, can be implemented using a dependency flow graph and prioritizing the next to-do items by how many inputs are available and how many inputs will be evicted from the cache by other inputs, temporaries, and outputs. You could do deeper analysis to find an even better schedule. It is an optimization problem; you need to estimate the cost of a better solution and its benefit.
Grid Order
While the usual example of loop tiling is matrix multiply, this example does not expose the full range of possibilities when tiling a 3D problem into a multilevel cache hierarchy.
Consider this problem: We have two data sets, where the points in each set are themselves vectors. For each pair of points, one from each data set, we want to compute their dot product. In this interesting case, assume each vector is too long to fit in the L1 cache.
We must perform A*B*N operations, each being two fetches and some arithmetic, in any order we prefer, where:
- A and B are the number of elements of the data sets
- N is the length of the vector
The following code tiles into both the L1 and the L2 caches. We chose an nStep small enough that the consecutive executions of the inner loop over n find the A[a,n] values are still in L1 from the previous loop.
void brick() {
for (int nLo = 0; nLo < nLen; nLo+=nStep) {
for (int bLo = 0; bLo < bLen; bLo+=bStep) {
for (int aLo = 0; aLo < aLen; aLo+=aStep) {
for (int a = aLo; a < std::min(aLo+aStep,aLen); a++) {
for (int b = bLo; b < std::min(bLo+bStep,aLen); b++) {
for (int n = nLo; n < std::min(nLo+nStep,aLen); n++) {
combine A[a,n] and B[b,n]
} } }
} } }
}The executions of the b-loop steadily load portions of B into the L2 cache. Instead of evicting the earlier Bs by loading too many of them, we stop after bStep of them are loaded, fetch the next portion of A, and combine it with all the Bs loaded so far. This loads some As into the cache as well, so instead of evicting all of them, we stop after aStep and combine those with the next set of Bs.
Done right, this reduces the total number of loads from main memory A*B*N to approximately (A+B)*N, which may change the algorithm from memory bound to compute bound – a huge win on a multi-core or many-core machine.
Tile Size
It is difficult to estimate how full you can get the cache before further loads evict useful data because:
- Each load evicts data from the cache.
- The mapping from virtual address to cache entry is somewhat random
- The caches vary in their associativity.
In addition, prefetching and vector sizes impact performance. For this reason, the best way to get the aStep, bStep, and nStep numbers is by experimentation.
Summary
The parent article, Why Efficient Use of the Memory Subsystem Is Critical to Performance, discussed many ways to efficiently use a memory subsystem, but tiling is by far the most effective (when it works) because it dramatically reduces the data movement in the slower or shared parts of the memory subsystem.
About the Author
Bevin Brett is a Principal Engineer at Intel Corporation, working on tools to help programmers and system users improve application performance. His visit to his daughter in Malawi, where she was serving with the Peace Corp, showed him the importance of education in improving lives. He hopes these educational articles help you improve lives.