Overview
In this article, I present a sample implementation of the famous MapReduce (MR) algorithm for persistent memory (PMEM), using the C++ bindings of libpmemobj, which is a core library of the Persistent Memory Development Kit (PMDK). The goal of this example is to show how PMDK facilitates implementation of a persistent memory aware MR with an emphasis on data consistency through transactions as well as concurrency using multiple threads and PMEM aware synchronization. In addition, I show the natural fault-tolerance capabilities of PMEM by killing the program halfway through and restarting it from where it left off, without the need for any checkpoint/restart mechanism. Finally, a sensitivity performance analysis is shown by varying the number of threads for both the map and reduce workers.
What is MapReduce?
MR is a programming model introduced by Google* in 2004 that uses functional programming concepts—inspired by the map and reduce primitives from languages such as Lisp*—to make it easier for programmers to run massively parallel computations on clusters composed of thousands of machines.
Since all functions are data-independent from one another, that is, all input data is passed by value, this programming paradigm has presented itself as an elegant solution for dealing with data consistency and synchronization issues. Parallelization can be achieved naturally by running multiple instances of functions in parallel. The MR model can be described as a subset of the functional programming model where all computations are coded using only two functions: map and reduce.

Figure 1: Overview of MapReduce. This figure is a modified version of Figure1 of the Google article referenced above.
A high-level overview of how MR works can be found in Figure 1. The input is composed of a set of files, which are split into chunks with a predefined size (usually between 16–64 MB). Each chunk is fed to a map task which creates key-value pairs that are grouped, sorted, and fed to a reduce task. Reduce tasks can then write their results directly to an output file, or pass them on to other reduce tasks for further reduction.
The typical example of a MR computation is word counting. Input chunks are split into lines. Each line then is fed to a map task which outputs a new key-value pair for each word found as follows: {key : 'word', value : '1'}. Reduce tasks then add all the values for the same key and create a new key-value pair with an updated value. If we have just one reduce task at the end, the output file will contain exactly one key-value entry per word with the value being the total count.
MapReduce Using PMEM
The way in which the MR model achieves FT is by storing its intermediate results in files residing in a local file system. This file system normally sits on top of either a traditional hard disk drive (HDD) or a solid state drive (SSD) attached to the node where the task that generates that data runs.
The first problem with this approach is of course the multiple orders of magnitude difference in bandwidth between these drives and volatile RAM (VRAM) memory. PMEM technology can narrow that gap significantly by running very close to VRAM speeds. Given this, one can consider as a first solution to simply switch from HDD or SSD to PMEM by mounting the local file system on top of a PMEM device. Although this surely helps, software still needs to be designed with a volatile-versus-persistent memory mentality. An example of this is when data has a different representation for VRAM (binary tree, heap, and so on) as it has for persistent storage (such as comma-separated values (CSV) files and structured query language (SQL) tables). This is where programming directly against PMEM using the library libpmemobj can greatly simplify development!
By programming directly against PMEM, the only thing needed to achieve FT is to specify what data structures should be permanent. Traditional VRAM may still be used for the sake of performance, but either in a transparent fashion (the same way processor caches are used relative to VRAM) or as a temporary buffer. In addition, a mechanism of transactions is put in place to make sure that permanent data structures do not get corrupted if a failure occurs in the middle of a write operation.
Design Decisions
This section describes the design decisions taken to make the sample PMEM aware.
Data Structures
This particular sample is designed to be run on one computer node only with one PMEM device attached to it. Workers are implemented as threads.
The first thing we need is a data structure that allows us to assign work to the map and reduce workers. This can be achieved with tasks. Tasks can be assigned to workers in either a (1) push fashion (from leader to workers), or a (2) pull fashion (workers fetch from the leader). In this example, the second option was chosen to simplify the implementation using a persistent list for tasks and a PMEM mutex for coordination between workers.
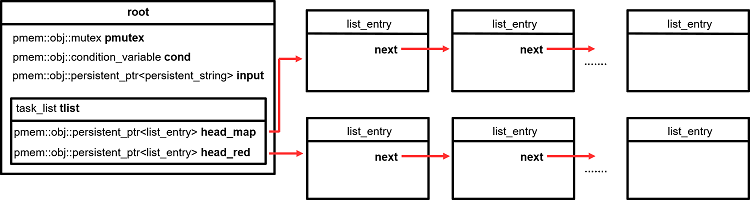
Figure 2: Root data structure.
The first object in a PMEM pool is always the root. This object serves as the main anchor to link all the other objects created in the program. In my case I have four objects. The first two are the pmem::obj versions of the C++ standard mutex and condition variable. We cannot use the standard ones because libpmemobj needs to be able to reset them in the event of a crash (otherwise a permanent deadlock could occur). For more information you can check the following article about synchronization with libpmemobj. The third object is the input data, which is stored as a one-dimensional persistent string. The fourth object is our list of tasks. You may have noticed that the variable tlist is not declared as a persistent pointer. The reason for this is that tlist is never modified (that is, overwritten) after it is first created, so there is no need to keep track of that memory range during transactions. The head variables of tlist for map and reduce tasks, on the other hand, are declared as persistent pointers because their values do in fact change during program execution (by adding new tasks).
Now, let’s take a look at the list_entry class:
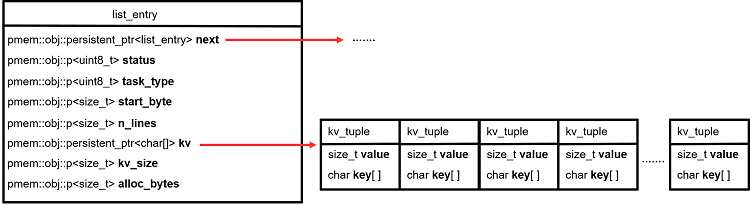
Figure 3: ListEntry class.
- The variable
nextis a persistent pointer to the next entry in the linked list. - The
statusflag can take the valuesTASK_ST_NEW(the task is new and a worker thread can start working on it right away),TASK_ST_BUSY(some thread is currently working on this task),TASK_ST_REDUCED(this task has the results of a reduction but it has not been combined with other reduced tasks yet) orTASK_ST_DONE(the task is finally done). - The
task_typeflag can take the valuesTASK_TYPE_NOTYPE,TASK_TYPE_MAPorTASK_TYPE_REDUCE. start_byteholds the chunk’s start byte in the input data string. Only relevant for map tasks.n_linesholds the number of lines in the chunk. Only relevant for map tasks.kvis a pointer for the list of key-value pairs. This list is only relevant for reduce tasks.kv_sizeis the size, in elements, of thekvlist.- Finally,
alloc_bytesis the size, in bytes, of thekvlist.
The reason why kv is a persistent pointer to char[] is due to performance considerations. Originally, I implemented this list as a linked list of kv_tuple pairs. However, due to the large amount of allocations (sometimes hundreds of thousands per thread per task) of very small objects (between 30–40 bytes on average), and given that allocations are synchronized by libpmemobj to protect the integrity of metadata, my code was not able to scale beyond eight threads. The change allows each thread to only do a single large allocation when storing all the key-value pairs for a single task.
You may have also noticed that I am not using the persistent_string class mentioned before for the key in kv_tuple. The reason is persistent_string is designed for persistent string variables that can change over time, so for each new string two persistent pointers are created: one for the object itself and one for the raw string. For this particular sample, the functionality of persistent_string is not needed. Key-value tuples are allocated in bulk and set during construction, and never changed until they are destroyed. This reduces the number of PMEM objects that the library needs to be aware of during transactions, effectively reducing overhead.
Nevertheless, allocating key-value tuples this way is a little bit tricky.
struct kv_tuple {
size_t value;
char key[];
};
Before creating the persistent list of key-value tuples, we need to calculate what its size will be in bytes. We can do that since the principal computation and sorting steps are completed first on VRAM, allowing us to know the total size in advance. Once we have done that, we can allocate all the PMEM needed with one call:
void
list_entry::allocate_kv (pmem::obj::pool_base &pop, size_t bytes)
{
pmem::obj::transaction::exec_tx (pop, [&] {
kv = pmem::obj::make_persistent<char[]> (bytes);
alloc_bytes = bytes;
});
}
Then, we copy the data to our newly created PMEM object:
void
list_entry::add_to_kv (pmem::obj::pool_base &pop, std::vector<std::string> &keys,
std::vector<size_t> &values)
{
pmem::obj::transaction::exec_tx (pop, [&] {
struct kv_tuple *kvt;
size_t offset = 0;
for (size_t i = 0; i < keys.size (); i++) {
kvt = (struct kv_tuple *)&(kv[offset]);
kvt->value = values[i];
strcpy (kvt->key, keys[i].c_str ());
offset
+= sizeof (struct kv_tuple) + strlen (kvt->key) + 1;
}
kv_size = keys.size ();
});
}
The input to this function—apart from the mandatory pool object pop (this object cannot be stored in persistent memory because it is newly created on each program invocation)—are two volatile vectors containing the key-value pairs generated by either a map or a reduce task. kv is iterated by means of a byte offset (first and last statements inside the for loop) because the size of each kv_tuple is not constant (it depends on the length of its key).
Synchronization
The following pseudocode represents the high-level logic of the worker threads:
- Wait until there are new tasks available.
- map workers work only on one task at a time.
- reduce workers try to work on two tasks (and combine them) if possible. If not, then work on one task.
- Work on task(s) and set to
TASK_ST_DONE(orTASK_ST_REDUCEDif it is a reduce worker working on a single task). - Store results in a newly created task with status
TASK_ST_NEW(the last task has the results for the whole computation and it is created directly asTASK_ST_DONE). - If computation is done (all tasks are
TASK_ST_DONE), then exit. - Go to (1).
Let’s take a look at step (1) for the map worker:
void
pm_mapreduce::ret_available_map_task (pmem::obj::persistent_ptr<list_entry> &tsk,
bool &all_done)
{
auto proot = pop.get_root ();
auto task_list = &(proot->tlist);
/* LOCKED TRANSACTION */
pmem::obj::transaction::exec_tx (
pop,
[&] {
all_done = false;
if ((task_list->ret_map (tsk)) != 0) {
tsk = nullptr;
all_done = task_list->all_map_done ();
} else
tsk->set_status (pop, TASK_ST_BUSY);
},
proot->pmutex);
}
The most important part of this snippet is located inside the transaction (inside the block started at pmem::obj::transaction::exec_tx). This transaction needs to be locked because each task should be executed by only one worker (realize that I am using the persistent mutex from the root object at the end of the transaction). The method task_list->ret_map() is called to check if a new map task is available and if so, we set its status to TASK_ST_BUSY, preventing it from being fetched by other workers. If no task is available, task_list->all_map_done()is called to check whether all map tasks are done, in which case the thread will exit (this is not shown in this code snippet).
Another important take-home lesson from this snippet is that every time a data structure is modified inside a locked region, the region should end at the same time as the transaction. If a thread changes a data structure inside a locked region and then fails right after it (but without finishing the transaction), all the changes done while locked are rolled back. At the same time this is happening, another thread may have acquired the lock and may be doing additional changes on top of the changes that the failed thread made (and are no longer meaningful), ultimately corrupting the data structure.
One way to avoid this is to lock the whole transaction by passing the persistent mutex to the transaction (as shown in the snippet above). There are cases, however, that this is not feasible (because the whole transaction is serialized de facto). In those cases, we can leave synchronized writes to the end of the transaction by putting them inside a nested locked transaction. Although nested transactions are flattened by default – which means that what we have at the end is just the outermost transaction – the lock from the nested transaction only locks the outermost one from the point where the nested transaction starts. This can be seen in the following snippet:
. . . . .
auto proot = pop.get_root ();
auto task_list = &(proot->tlist);
pmem::obj::transaction::exec_tx (pop, [&] {
. . . . . .
/* This part of the transaction can be executed concurrently
* by all the threads. */
. . . . . .
pmem::obj::transaction::exec_tx (
pop,
[&] {
/* this nested transaction adds the lock to the outer one.
* This part of the transaction is executed by only one
* thread at a time */
task_list->insert (pop, new_red_tsk);
proot->cond.notify_one ();
tsk->set_status (pop, TASK_ST_DONE);
},
proot->pmutex); /* end of nested transaction */
}); /* end of outer transaction */
The case (1) for the reduce worker is more complex, so I will not reproduce it here in its entirety. Nevertheless, there is one part that is worth some discussion:
void pm_mapreduce::ret_available_red_task (
pmem::obj::persistent_ptr<list_entry> (&tsk)[2], bool &only_one_left,
bool &all_done)
{
auto proot = pop.get_root ();
auto task_list = &(proot->tlist);
/* locked region */
std::unique_lock<pmem::obj::mutex> guard (proot->pmutex);
proot->cond.wait (
proot->pmutex,
[&] { /* conditional wait */
. . . . .
});
. . . . .
guard.unlock ();
The main difference between my map and reduce workers is that reduce workers perform a conditional wait. Map tasks are created at once and before computation starts. Hence, map workers do not need to wait for new tasks to be created. Reduce workers, on the other hand, conditionally wait until other workers create new reduce tasks. When a reduce worker thread is woken up (another worker runs proot->cond.notify_one()after a new task is created and inserted in the list), a boolean function (passed to proot->cond.wait()) runs to check whether the worker should continue or not. A reduce worker will continue when either (a) at least one task is available or (b) all tasks are finally done (the thread will exit).
Fault Tolerance
The sample code described in this article can be downloaded from GitHub*. This code implements a PMEM version of the wordcount program by doing inheritance from the general PMEM MapReduce class and completing the virtual functions map() and reduce():
class pm_wordcount : public pm_mapreduce
{
public:
/* constructor */
pm_wordcount (int argc, char *argv[]) : pm_mapreduce (argc, argv) {}
/* map */
virtual void
map (const string line, vector<string> &keys, vector<size_t> &values)
{
size_t i = 0;
while (true) {
string buf;
while (i < line.length ()
&& (isalpha (line[i]) || isdigit (line[i]))) {
buf += line[i++];
}
if (buf.length () > 0) {
keys.push_back (buf);
values.push_back (1);
}
if (i == line.length ())
break;
i++;
}
}
/* reduce */
virtual void
reduce (const string key, const vector<size_t> &valuesin,
vector<size_t> &valuesout)
{
size_t total = 0;
for (vector<size_t>::const_iterator it = valuesin.begin ();
it != valuesin.end (); ++it) {
total += *it;
}
valuesout.push_back (total);
}
};
Build Instructions
To compile the mapreduce code sample, just type make mapreduce from the root of the pmem/pmdk-examples GitHub repository. For more information, read the mapreduce sample README file.
Instructions to Run the Sample
After compilation, you can run the program without parameters to get usage help:
$ ./wordcount
USE: ./wordcount pmem-file <print | run | write -o=output_file | load -d=input_dir> [-
m=num_map_workers] [-nr=num_reduce_workers]
command help:
print -> Prints mapreduce job progress
run -> Runs mapreduce job
load -> Loads input data for a new mapreduce job
write -> Write job solution to output file
command not valid
To see how FT works, run the code with some sample data. In my case, I use all of the Wikipedia abstracts (the size of the file is 5GB so it may take a long time to load in your browser; you can download it by doing right-click > save as). The first step before running MR is loading the input data to PMEM:
$ ./wordcount /mnt/mem/PMEMFILE load -d=/home/.../INPUT_WIKIABSTRACT/
Loading input data
$
Now we can run the program (in this case I use two threads for map and two threads for reduce workers). After some progress has been made, let’s kill the job by pressing Ctrl-C:
$ ./wordcount /mnt/mem/PMEMFILE run -nm=2 -nr=2
Running job
^C% map 15% reduce
$
We can check the progress with the command print:
$ ./wordcount /mnt/mem/PMEMFILE print
Printing job progress
16% map 15% reduce
$
So far, our progress has been saved! If we use the command run again, computation will start where we left off (16% map and 15% reduce):
$ ./wordcount /mnt/mem/PMEMFILE run -nm=2 -nr=2
Running job
16% map 15% reduce
When computation is done, we can dump the results (command write) to a regular file and read the results:
$ ./wordcount /mnt/mem/PMEMFILE write -o=outputfile.txt
Writing results of finished job
$ tail -n 10 outputfile.txt
zzeddin 1
zzet 14
zzeti 1
zzettin 4
zzi 2
zziya 2
zzuli 1
zzy 1
zzz 2
zzzz 1
$
Performance
The system used has an Intel® Xeon® Platinum 8180 processor CPU with 28 cores (224 threads) and 768 GB of Intel® Double Data Rate 4 (Intel® DDR 4) RAM. To emulate a PMEM device mounted at /mnt/mem, 512 GB of RAM is used. The operating system used is CentOS Linux* 7.3 with kernel version 4.9.49. The input data used is again all of the Wikipedia abstracts (5 GB). In the experiments, I allocate half of the threads for map and half for reduce tasks.
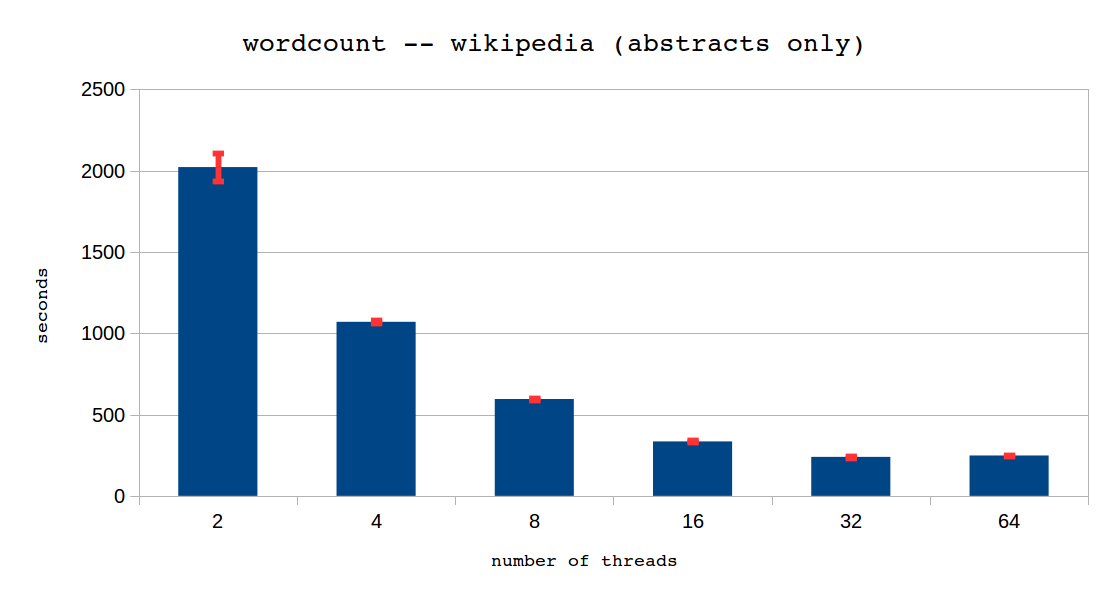
Figure 4: Time taken to count the words in all of the Wikipedia abstracts (5 GB) using our PMEM-MR sample.
As it is possible to see, our sample scales well (approximately halving completion time), all the way to 16 threads. An improvement is still observed with 32 threads, but of only 25 percent. With 64 threads we reach the scalability limits for this particular example. This is because the synchronization parts become a larger share of the total execution time as more threads are used with the same data.
Summary
In this article, I have presented a sample implementation of the famous MR algorithm using the C++ bindings of the PMEM library libpmemobj. I showed how to achieve data consistency through transactions and concurrency using a PMEM mutex and conditional variable. I have also shown how PMDK—by allowing the programmer to code directly against PMEM (that is, by defining what data structures should be persisted)—facilitates the creation of programs that are naturally FT. Finally, I finished the article with a sensitivity performance analysis showing scalability when more threads are added to the execution.
About the Author
Eduardo Berrocal joined Intel as a Cloud Software Engineer in July 2017 after receiving his PhD in Computer Science from Illinois Institute of Technology (IIT) in Chicago, Illinois. His doctoral research interests were focused on (but not limited to) data analytics and fault tolerance for high performance computing. In the past he worked as a summer intern at Bell Labs (Nokia), as a research aide at Argonne National Laboratory, as a scientific programmer and web developer at the University of Chicago, and as an intern in the CESVIMA laboratory in Spain.
Resources
- MapReduce: Simplified Data Processing on Large Clusters, Jeffrey Dean and Sanjay Ghemawat
- Parallel Programming Using Skeleton Functions, J. Darlington, et al., Dept. of Computer Science, University of Western Australia
- Persistent Memory Programming, pmemobjfs - The simple FUSE based on libpmemobj, September 29, 2015
- Persistent Memory Programming, C++ bindings for libpmemobj (part 7) - synchronization primitives, May 31, 2016
- Persistent Memory Programming, Modeling strings with libpmemobj C++ bindings, January 23, 2017
- link to sample code in GitHub*
- pmem.io Persistent Memory Programming, How to emulate Persistent Memory, February 22, 2016