Usable Post-Training 4-Bit Quantization for Deep Learning Networks

AUTHOR:
Ron Banner
Yury Nahshan

Deep learning networks can require significant bandwidth and storage for intermediate computations, in addition to substantial computing resources. Network quantization to lower numerical precision can reduce the burden of intermediate results, but with a reduction in model accuracy that could in the past only be recovered by using the original training data set for additional training or fine tuning.

In research being presented at NeurIPS 2019 ^[1], we propose the first practical 4-bit post-training quantization approach, which does not involve retraining to fine-tune the quantized model or the full dataset used for earlier training. We suggest quantizing both activations and weights and offer three complementary methods for minimizing quantization error at the tensor level. Combining these methods, we achieve accuracy of just a few percent less than state-of-the-art baselines across a wide range of models. This result may point towards opportunities to fit more capable, performant neural networks into more tightly constrained inference hardware by facilitating easier 4-bit post-training quantization.

Background

Deep learning models are well-known for being computationally costly. Huge amounts of data must be passed through a neural network in order to train it. Following training, inference using that network must be executed rapidly in order to provide useful results. Therefore, reducing the compute overhead of deep learning training and inference is an area of vibrant theoretical investigation, with the quantization of neural networks to lower precision being one of the primary approaches. For example, with hardware support such as Intel® Deep Learning Boost (Intel® DL Boost), a feature of second-generation Intel® Xeon® Scalable processors, lower-precision deep learning networks execute more calculations per second, reduce memory bandwidth and power consumption, and offer the ability to fit a larger network onto a target device.

Most earlier studies into the quantization of neural networks have involved either training a quantized network from scratch ^[2] or creating a quantized model by re-training (fine-tuning) a model that was already trained with higher precision at an earlier time ^[3]. While additional training has a good ability to compensate for model accuracy lost as a result of quantization, it has drawbacks that reduce its real-world utility. If the original training data is not easily accessible due to data privacy, ownership, or size, then additional training is not possible. Further, even if the training data is available, additional training is expensive in terms of time for optimization, requiring skilled labor, and demand for compute.

With these constraints, it is often desirable to reduce overall model size by quantizing weights and activations after the model has been trained but without re-training or fine-tuning the model. Methods to accomplish this are known as post-training quantization and are beneficial for their ease of use (compared to additional training) and support for quantization with limited data. Models quantized to 8-bit precision after training can produce near-floating-point accuracy in several popular models, e.g., ResNet, VGG, and AlexNet, and have seen coverage in recent industrial publications. ^[4,5,6,7] At the same time, methods of quantization for numerical precisions of 4-bits and below have been shown to be effective, but are subject to the same hindrances that have impeded other quantization efforts. ^[8,9,10,11]

Reducing Accuracy Degradation at 4-Bit Precision

We have found that post-training quantization to 4-bit precision with just a few percent accuracy degradation may be possible. In order to accomplish this, we have sought to minimize local errors introduced during the quantization process (e.g., round-off errors) via knowledge of the statistical characterization of neural network distributions, which tend to have a bell-curved distribution around the mean. This enables the design of efficient quantization schemes that minimize the mean-squared quantization error at the tensor level without retraining.

We make three contributions for post-training quantization:

1. Analytical Clipping for Integer Quantization (ACIQ): We propose limiting (or “clipping”) the range of activations within the tensor. While this distorts the original tensor, it reduces the rounding error in the part of the distribution that contains most of the information. We approximate the optimal clipping value analytically from the tensor’s distribution by minimizing the mean-square-error measure. This approximation is easy to use during runtime and can easily be integrated with other quantization techniques.
2. Per-channel bit allocation: We introduce a bit allocation policy to determine the optimal bit-width for each channel. Given a constraint on the average per-channel bit-width, our goal is to allocate for each channel the desired bit-width representation so that overall mean-square-error is minimized. We solve this problem analytically and show that by taking certain assumptions about the input distribution, the optimal quantization step size of each channel is proportional to the 2/3-power of its range.
3. Bias-correction: We observe an inherent bias in the mean and the variance of the weight values following their quantization. We suggest a simple method to compensate for this bias.

We evaluated these methods on six ImageNet models. The methods were used as follows:

• ACIQ for activation quantization
• Bias-correction for weight quantization
• Per-channel bit allocation for both weight and activation quantization

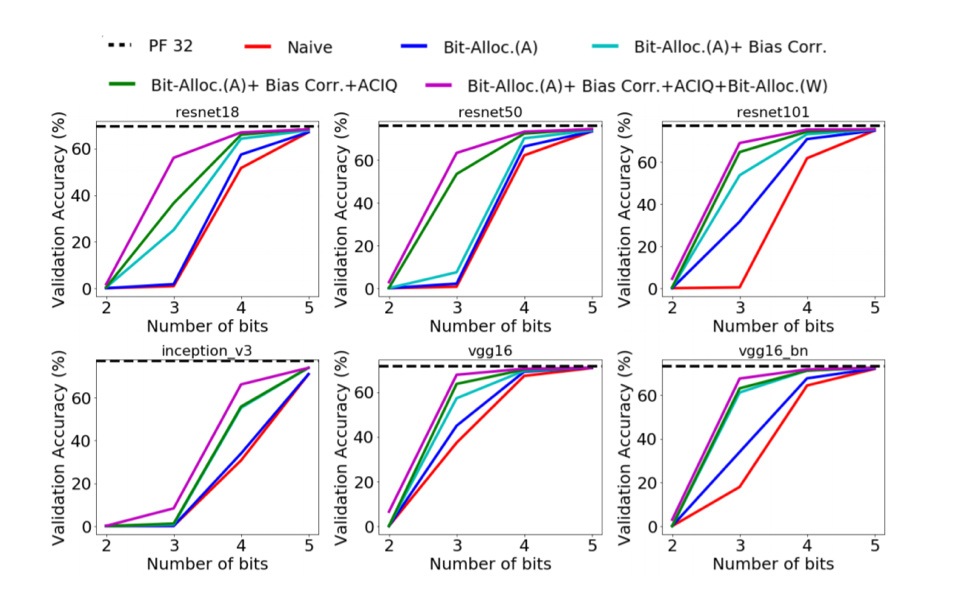
Figure 1: An ablation study showing the methods work in synergy and effectively at 3-4 bit precision.

Results

We found that when all three methods were used in combination, accuracy degradation due to quantization is preserved even for aggressive quantization. In Figure 1, we demonstrate the interaction between these methods at different quantization levels for various models.

Our findings suggest that additional training may be unnecessary for 4-bit quantization, which would enable much more broad usage of this method. In the applied setting, 4-bit quantization and similar approaches may help developers deliver more capable deep learning algorithms within the constraints of the target hardware.

For more on this research, please review our paper, “Post training 4-bit quantization of convolutional networks for rapid-deployment,” look for us at the 2019 NeurIPS conference, and stay tuned to @IntelAIResearch on Twitter.

^[1] We thank our co-author and co-presenter Daniel Soudry of Technion’s Israel Institute of Technology.

^[2] Hubara, I, Courbariaux, M, Soudry, D., El-Yaniv, R., and Bengio, Y. Binarized neural networks. In NIPS. US Patent 62/317,665, Filed, 2016.

^[3] Han, Song, Mao, Huizi, and Dally, William J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149, 2015.

^[4] Goncharenko, Alexander, Denisov, Andrey, Alyamkin, Sergey, and Terentev, Evgeny. Fast adjustable threshold for uniform neural network quantization. arXiv preprint arXiv:1812.07872, 2018.

^[5] Choukroun, Yoni, Kravchik, Eli, and Kisilev, Pavel. Low-bit quantization of neural networks for efficient inference. arXiv preprint arXiv:1902.06822, 2019.

^[6] Meller, Eldad, Finkelstein, Alexander, Almog, Uri, and Grobman, Mark. Same, same but different recovering neural network quantization error through weight factorization. arXiv preprint arXiv:1902.01917, 2019.

^[7] Migacz, S. 8-bit inference with tensorrt. In GPU Technology Conference, 2017.

^[8] Lin, Xiaofan, Zhao, Cong, and Pan, Wei. Towards accurate binary convolutional neural network. In Advances in Neural Information Processing Systems, pp. 345–353, 2017.

^[9] McKinstry, Jeffrey L, Esser, Steven K, Appuswamy, Rathinakumar, Bablani, Deepika, Arthur, John V, Yildiz, Izzet B, and Modha, Dharmendra S. Discovering low-precision networks close to fullprecision networks for efficient embedded inference. arXiv preprint arXiv:1809.04191, 2018.

^[10] Zhou, Shuchang, Wu, Yuxin, Ni, Zekun, Zhou, Xinyu, Wen, He, and Zou, Yuheng. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv preprint arXiv:1606.06160, 2016.

^[11] Choi, Jungwook, Wang, Zhuo, Venkataramani, Swagath, Chuang, Pierce I-Jen, Srinivasan, Vijayalakshmi, and Gopalakrishnan, Kailash. Pact: Parameterized clipping activation for quantized neural networks. arXiv preprint arXiv:1805.06085, 2018.

Intel technologies’ features and benefits depend on system configuration and may require enabled hardware, software or service activation. Performance varies depending on system configuration. No computer system can be absolutely secure. Check with your system manufacturer or retailer or learn more at intel.com.

© Intel Corporation. Intel, the Intel logo, and other Intel marks are trademarks of Intel Corporation or its subsidiaries. Other names and brands may be claimed as the property of others.